今回は、オフェンスとディフェンスの各種スタッツを使って、統計ソフトRによるデータの散らばりの尺度を算出する方法を紹介していきます。
データは、2022–23レギュラーシーズンのPbox(過去記事参照)をベースに、カンファレンス・ファイナルに進出した4チームのものを使用していきます。
まずは、今回算出するデータの散らばりの尺度について確認していきたいと思います。
※データ分析を実践する際に参考にしている書籍『Basketball Data Science: With Applications in R』の紹介記事も書きましたので、よろしければご確認ください。
データの散らばりの尺度
ここでは、総務省統計局「データの散らばりを捉える」や統計WEBサイト「6-4. 変動係数」を参考にしながら、データの散らばりの尺度を簡単に紹介していきます。
範囲(レンジ)
範囲(レンジ)とは、データの分布の幅(散らばり)を示す尺度で、具体的にはデータの最大値と最小値の差で求められます。
範囲(レンジ)は散らばりの尺度としてかなり単純なものであり、外れ値の影響を受けやすいという欠点もあります。
変動係数(Coefficient of Variation)
変動係数(Coefficient of Variation)とは、標準偏差の平均に対する相対的な比を言い、「変動係数=標準偏差÷平均」で求められます。
変動係数は単位を持たない尺度のため、異なる単位をもつデータを比較するのに適しています。
続いて、実際のスタッツを使ってデータの散らばりの尺度を算出し、グラフを作成していきます。
セルティックス、ヒート、ナゲッツ、レイカーズのスタッツの散らばり具合を確認
ボストン・セルティックスのスタッツ<ジェイソン・テイタムが得点源>
セルティックスの各スタッツの散らばりを示すグラフは下記のとおりです。
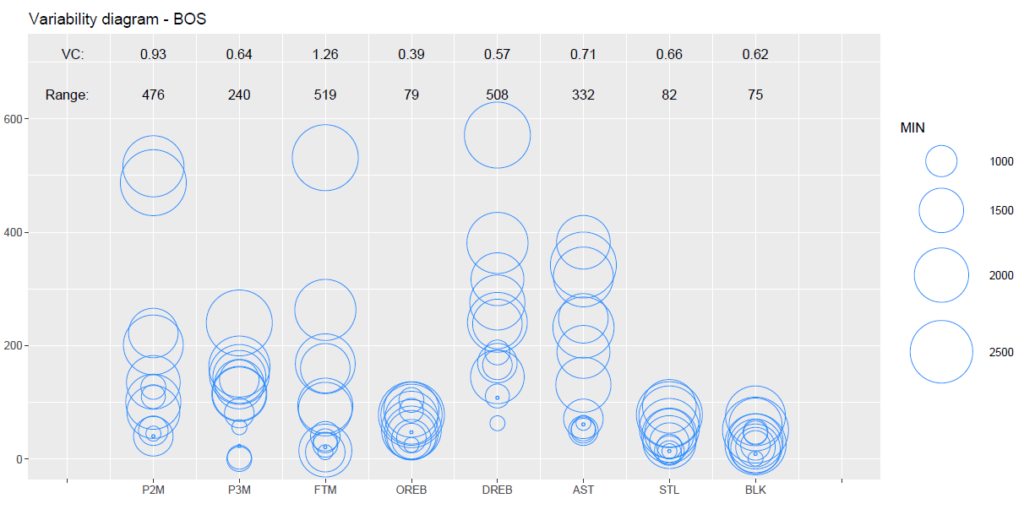
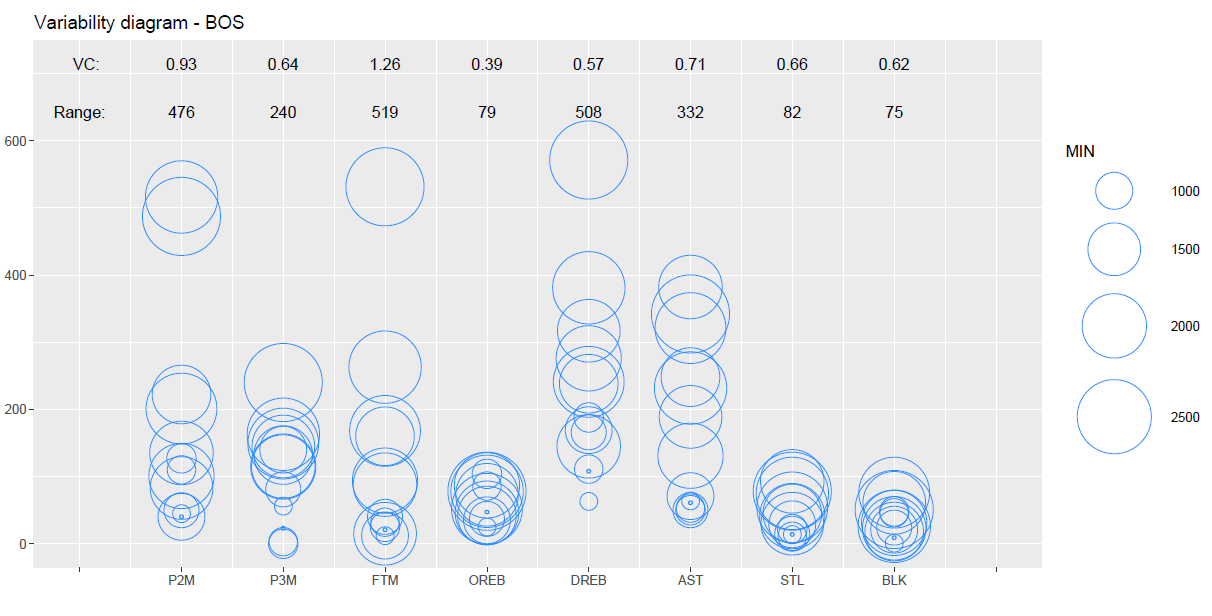
上記のグラフでは、縦軸にスタッツの数値が表示され、各列にある円の中心は各プレイヤーの実際のスタッツ数と対応しています。
円の大きさは各プレイヤーの出場時間の長さを表しており、グラフ作成の際には500MIN(分)以上のプレイヤーのみを抽出しています。
グラフの表示に関しては、左から順にP2M(2Pシュート成功数)、P3M(3Pシュート成功数)、FTM(フリースロー成功数)、OREB(オフェンスリバウンド数)、DREB(ディフェンスリバウド数)、AST(アシスト数)、STL(スティール数)、BLK(ブロック数)を示しています。
なお、グラフの上部分で示されているVCの数値は変動係数(Coefficient of Variation)を表し、Rangeの数値は範囲(レンジ)を表しています。
また、上記のグラフのベースとなるスタッツの表は下記のとおりです。
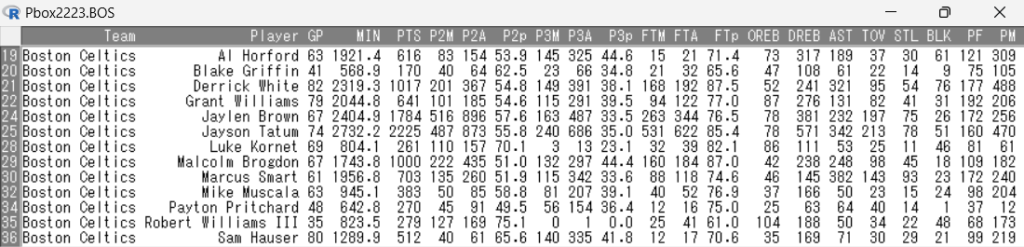
上記のグラフを確認すると、フリースロー成功数の変動係数が1.26となっており、チームのスタッツの中ではデータの散らばり方が最も大きくなっていることが分かります。
上記の表で実際のスタッツを確認すると、フリースロー成功数のトップはジェイソン・テイタムの531本で、2位のジェイレン・ブラウンの263本を大きく引き離しています。
フリースロー成功数の最小本数は、ペイトン・プリチャードとサム・ハウザーの12本であり、その範囲(レンジ)は519本(最大本数と最小本数の差)であることが分かります。
また、2Pシュート成功数の散らばりも比較的大きく、変動係数は0.93となっています。
こちらも実際のスタッツを確認すると、2Pシュート成功数のトップはジェイレン・ブラウンの516本、その次にジェイソン・テイタムの487本が続きます。
セルティックスに関しては、2Pシュートとフリースローによる得点がジェイソン・テイタムとジェイレン・ブラウンに偏ることで、データの散らばりが大きくなっていることが確認できます。
一方で、散らばりが最も小さいスタッツはオフェンスリバウンド数で、変動係数は0.39となっています。
なお、上記のグラフを出力するためのコマンドは下記のとおりです。
Pbox2223 <- read.csv(file="Pbox_2223.csv") #データファイルPbox2223を読み込み
Pbox2223.BOS <- subset(Pbox2223, Team=="Boston Celtics" & MIN>=500) #Pbox2223からBOSで出場時間500MIN以上のプレイヤーを抽出
vrbBOS <- variability(data=Pbox2223.BOS, data.var=c("P2M", "P3M", "FTM", "OREB", "DREB","AST","STL","BLK"), size.var=c("MIN"))
# variability関数で標準偏差、レンジ、変動係数を算出しvrbBOSへ格納
plot(vrbBOS, title="Variability diagram - BOS") #データをvrbBOSに指定しグラフをプロット
マイアミ・ヒートのスタッツ<攻守においてアデバヨが活躍>
ヒートの各スタッツの散らばりを示すグラフは下記のとおりです。
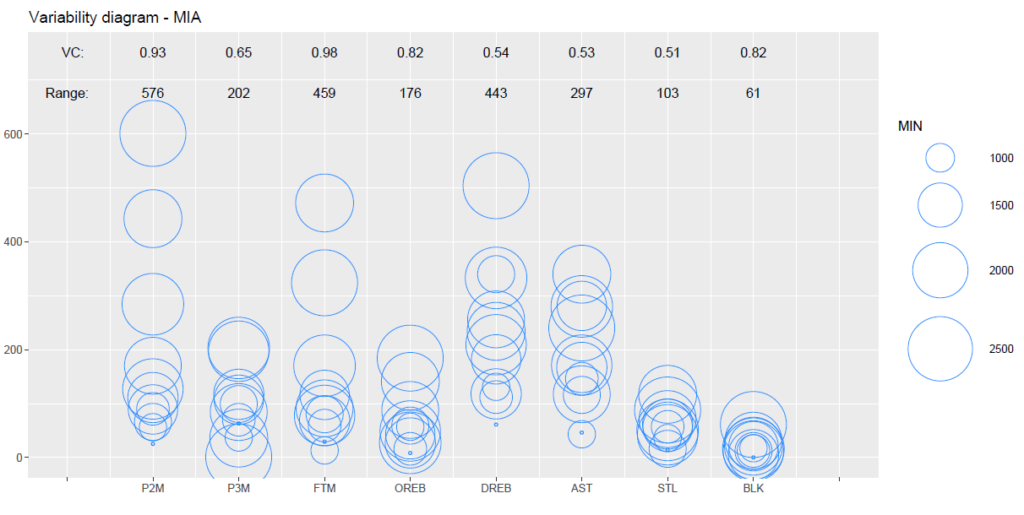
また、上記のグラフのベースとなるスタッツの表は下記のとおりです。
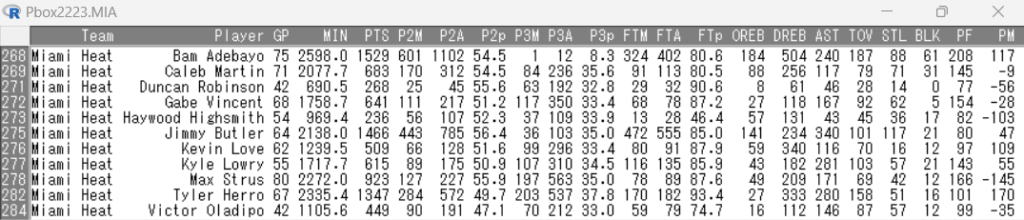
上記のグラフを確認すると、最も変動係数が大きいのはフリースロー成功数の0.98であり、フリースロー成功数のトップはジミー・バトラーの472本、次にバム・アデバヨの324本が続きます。
また、2Pシュート成功数に関しても、変動係数が0.93であり散らばりが大きいことが分かります。
2Pシュート成功数のトップはバム・アデバヨの601本で、次にジミー・バトラーの443本が続きます。
オフェンス面では、アデバヨとジミー・バトラーが得点源となっており、2人からの得点に偏ることでデータの散らばりが大きくなっていることが確認できます。
さらに、オフェンスリバウンド数とブロック数の変動係数も比較的高く、その値はともに0.82となっています。
実際のスタッツを確認すると、オフェンスリバウンド数のトップはアデバヨの184本、ブロック数のトップもアデバヨの61本となっています。
アデバヨに関しては攻守において存在感が強く、複数のスタッツがアデバヨに偏ることでデータの散らばりが大きくなっていることが考えられます。
一方で、変動係数が最も少ないのはスティール数で、その値は0.51となっています。
ヒートのスティールに関しては、下記の記事でチーム全体のスティールが多いことを確認していますので、よろしければあわせてご覧ください。
なお、上記のグラフを出力するためのコマンドは下記のとおりです。
Pbox2223.MIA <- subset(Pbox2223, Team=="Miami Heat" & MIN>=500)
vrbMIA <- variability(data=Pbox2223.MIA, data.var=c("P2M", "P3M", "FTM", "OREB", "DREB","AST","STL","BLK"), size.var=c("MIN"))
plot(vrbMIA, title="Variability diagram - MIA")
デンバー・ナゲッツのスタッツ<ヨキッチがアシストでけん引>
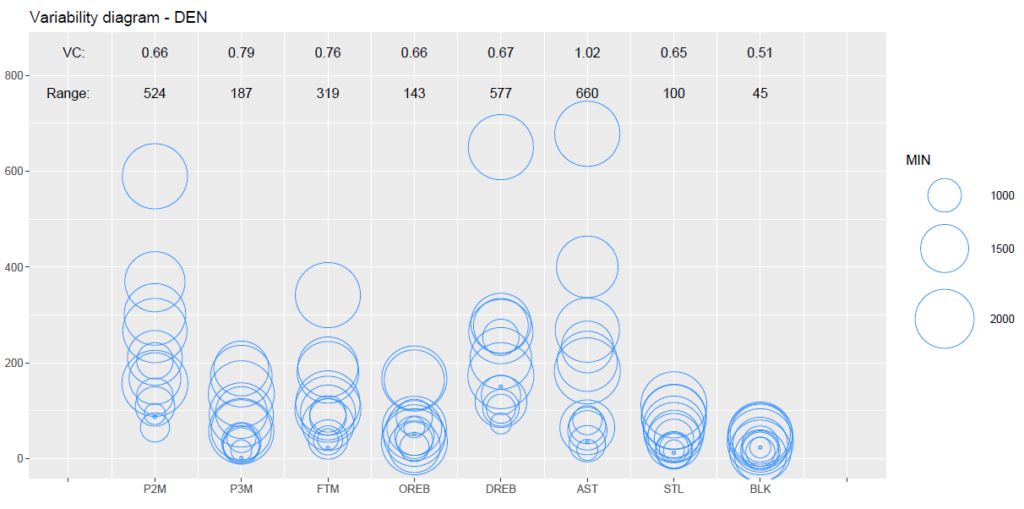
ナゲッツの各スタッツの散らばりを示すグラフは下記のとおりです。
また、上記のグラフのベースとなるスタッツの表は下記のとおりです。
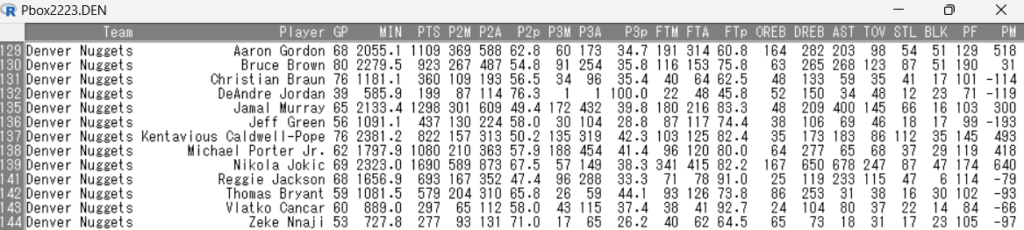
上記のグラフを確認すると、最も変動係数が大きいのはアシスト数の1.02となっています。
アシスト数のトップはニコラ・ヨキッチの678本となっており、アシストがヨキッチに偏ることでデータの散らばりが大きくなっていることが読み取れます。
また、3ポイントシュート成功数とフリースロー成功数の変動係数も比較的大きな値をとっており、それぞれ0.79と0.76を示しています。
実際のスタッツは、3ポイントシュート成功数はマイケル・ポーターJr.の188本がトップで、フリースロー成功数のほうはニコラ・ヨキッチの341本がトップです。
一方、変動係数が最も少ないのはブロック数の0.51で、データの散らばりが最も小さいことが分かります。
なお、上記のグラフを出力するためのコマンドは下記のとおりです。
Pbox2223.DEN <- subset(Pbox2223, Team=="Denver Nuggets" & MIN>=500)
vrbDEN <- variability(data=Pbox2223.DEN, data.var=c("P2M", "P3M", "FTM", "OREB", "DREB","AST","STL","BLK"), size.var=c("MIN"))
plot(vrbDEN, title="Variability diagram - DEN")
ロサンゼルス・レイカーズのスタッツ<アンソニー・デイビスが好スタッツ>
レイカーズの各スタッツの散らばりを示すグラフは下記のとおりです。
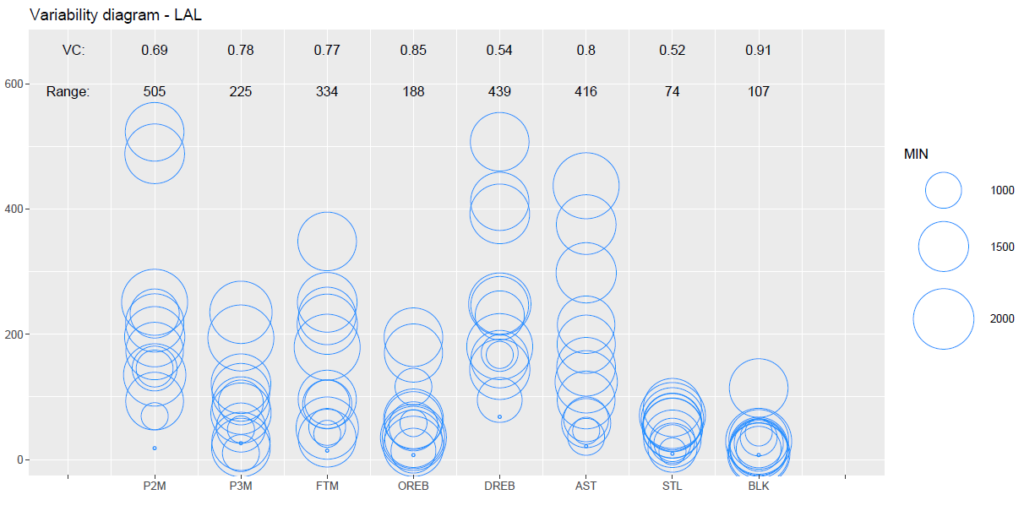
また、上記のグラフのベースとなるスタッツの表は下記のとおりです。
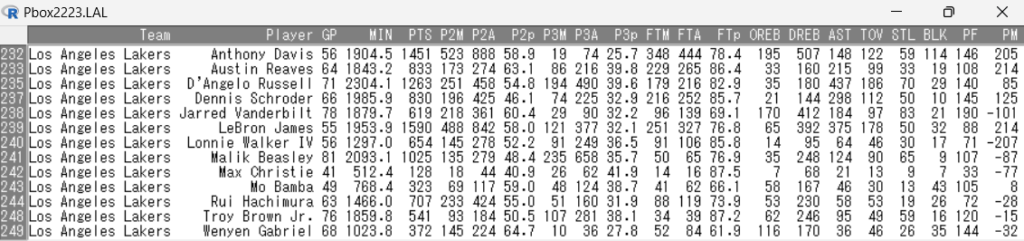
最も変動係数が大きいのはブロック数の0.91であり、ブロック数のトップはアンソニー・デイビスの114本となっています。
続いて、オフェンスリバウンドの変動係数0.85が大きく、オフェンスリバウンド数のトップもアンソニー・デイビスで195本となっています。
また、フリースロー成功数の変動係数0.77も比較的大きな値を示しており、実際のスタッツを確認すると、こちらもトップはアンソニー・デイビスで本数は348本です。
レイカーズに関しては、複数のスタッツがアンソニー・デイビスに偏ることでデータの散らばりが大きくなっていることが読み取れます。
なお、スティール数については変動係数が0.52となっていることから、最もデータの散らばりが小さいスタッツであることが分かります。
※ アシスト数については、ディアンジェロ・ラッセルのミネソタ・ティンバーウルブズ在籍時のスタッツ分までまとめられて集計されているため、変動係数0.8はあくまでも参考値扱いとしています。また、3ポイントシュート成功数についても、マリーク・ビーズリーのユタ・ジャズ在籍時のスタッツ分までまとめられて集計されているため、変動係数0.78はあくまでも参考値扱いとしています。
また、上記のグラフのベースとなるスタッツの表は下記のとおりです。
Pbox2223.LAL <- subset(Pbox2223, Team=="Los Angeles Lakers" & MIN>=500)
vrbLAL <- variability(data=Pbox2223.LAL, data.var=c("P2M", "P3M", "FTM", "OREB", "DREB","AST","STL","BLK"), size.var=c("MIN"))
plot(vrbLAL, title="Variability diagram - LAL")
おわりに
今回はデータの散らばりの尺度を使って、2022-23シーズンのカンファレンス・ファイナルに進出した4チームの各スタッツの散らばりを確認しました。
チームごとのデータの散らばりを数値化・グラフ化することで、スタッツが特定のプレイヤーに偏っているかどうかが視覚的にもわかりやすくなったと思います。
チーム内で役割が明確にされているようなスタッツ(アシストや3Pシュートなど)に関しては、データの散らばりが大きくなる傾向があるかもしれませんが、各チームの特徴を捉える方法の一つとして、データの散らばりを確認することは大事なことだと思いました。
なお、本記事は、記事の最後に紹介している書籍を参考にして作成しています。
それでは、今回のトラッシュトークは以上です。
【参考書籍】
Paola Zuccolotto and Marica Manisera (2020), Basketball Data Science – with Applications in R. Chapman and Hall/CRC. ISBN 9781138600799.
※本書籍の紹介記事を書いていますので、よろしければご参考ください。
倉田 博史、星野 崇宏(2009)『入門統計解析』新世社.