※ 当サイトは、アフィリエイト広告を利用しています。

【2025 NBAファイナル】サンダーとペイサーズの“勝ち筋”を分解する――集中と分散、ふたつの戦略的チーム設計

2025.06.03
記事内に広告が含まれています。

データ分析を実践する際に参考にしている書籍『Basketball Data Science: With Applications in R』の紹介記事も書いていますので、よろしければご確認ください。

Basketball Data Science: With Applications in R (Chapman & Hall/CRC Data Science Series) (English Edition)
YouTube
★ YouTubeチャンネルも運営中！ ★
当ブログの記事内容を動画で分かりやすく解説しています。
▶ チャンネルはこちら
目次
  1. 🏀【　導入　】
  2. 📊【　両チームはどんなスタッツ特性を持っているのか？　】
    1. ＜チームスタッツで見る全体像＞
      1. 　オフェンス・ディフェンス効率 ＆ 試合テンポ
      2. 　攻撃の質：Four Factorsから見る特徴
      3. 　守備の質：相手の攻撃をどこまで抑えているか
      4. 　小まとめ：両チームのスタッツから見える方向性
  3. 🔀【　ペイサーズのオフェンス構造は、なぜ“分散型”なのか？　】
    1. ＜アシストネットワークと得点分布から見える主力と分散＞
      1. 　アシストネットワークとプレイヤーの役割分担
      2. 　ASTPTSとFGPTSの関係性（散布図）
      3. 　得点分布の“分散性”──ジニ係数と実際のスコアリング
      4. 　小まとめ：全員で得点する“分散型”オフェンス
  4. 👥【　サンダーのオフェンス構造は、なぜ“役割分担型”なのか？　】
    1. ＜アシストネットワークと得点分布から見える役割集中と分担＞
      1. 　アシストネットワークと散布図から見る“二枚看板”と分担
      2. 　ASTPTSとFGPTSの関係性（散布図）
      3. 　得点分布の集中度とジニ係数
      4. 　役割集中の合理性──“守備型”メンバーの台頭
      5. 　小まとめ：役割分担が生む“攻守両立型”チーム体制
  5. 両チームの“構造”は、どんな勝ち筋に繋がっているのか？
    1. ＜分散と集中、それぞれの効率のかたち＞
      1. 　分散型（ペイサーズ）：多様性と耐性
      2. 　集中型（サンダー）：エースの最大化と役割分担
      3. 　“分散と集中”──二つの効率モデル
      4. 　小まとめ
  6. 🔚【　おわりに　】
  7. ※参考＜統計ソフトRに入力するコマンド＞

🏀【　導入　】

2025年NBAファイナルは、インディアナ・ペイサーズとオクラホマシティ・サンダーの顔合わせとなりました。両チームとも高い得点力を持ちながら、その“オフェンスの作り方”や“勝ち筋”は対照的です。

本記事では、「分散型」と「集中型」という正反対のチーム構造がスタッツやチャートでどう可視化されるのか、そしてNBAファイナルという最高の舞台でその設計思想がどのように“強み”や“勝ち筋”につながっているのかを、データから深掘りします。

📊【　両チームはどんなスタッツ特性を持っているのか？　】

プレーオフに入っても高い得点効率を維持しているインディアナ・ペイサーズとオクラホマシティ・サンダー。しかし、そのオフェンスの成り立ちや勝ち方のスタイルはまったく異なります。

まずはチーム全体のスタッツを俯瞰しながら、両チームの攻守における「強み」や「違い」がどこにあるのかを確認していきましょう。

＜チームスタッツで見る全体像＞

両チームのプレーオフでの基本的なチームスタッツ（1試合平均）を、3つの観点に分けて比較します。

　オフェンス・ディフェンス効率 ＆ 試合テンポ

チームOffRtg
（オフェンス効率）		DefRtg
(ディフェンス効率)		NetRtg
（差引）		PACE
（試合テンポ）
ペイサーズ117.7（2位）113.6（9位）+4.1（4位）98.4（3位）
サンダー115.9（3位）104.7（1位）+11.2（2位）100.6（2位）
※スタッツはNBA公式より参照。

🔍 解説：

  • ペイサーズはオフェンス効率が高くテンポも速いチームで、点の取り合いを好むスタイル。
  • 対するサンダーは、リーグ随一のディフェンス効率（DefRtg 1位）と、テンポも速い構造。守って走るチーム像が浮かびます。

　攻撃の質：Four Factorsから見る特徴

チームeFG%FTA RateTOV%OREB%
ペイサーズ57.6（1位）0.279（5位）12.7（3位）23.8（16位）
サンダー53.2（6位）0.261（9位）11.6（1位）28.5（11位）
※スタッツはNBA公式より参照。

🔍 解説：

  • ペイサーズはeFG%で1位、TOV%でも3位と、シュート効率とミスの少なさが際立つチーム。
  • 一方、オフェンスリバウンド（OREB%）は最下位（16位）で、基本的に“ワンチャンス”で得点する構造。
  • サンダーはTOV% 1位＝最もボールを失わないチーム。
  • OREBやFTAでもある程度の加点力があり、攻撃における“安定と粘り”が特徴です。

　守備の質：相手の攻撃をどこまで抑えているか

チームOpp eFG%Opp FTA RateOpp TOV%Opp OREB%
ペイサーズ52.2（5位）0.326（15位）14.2（8位）31.6（11位）
サンダー49.9（2位）0.273（11位）17.7（1位）32.7（12位）
※スタッツはNBA公式より参照。

🔍 解説：

  • サンダーは相手のeFG%を抑え（Opp eFG% 2位）、TOVを最も多く奪う守備（Opp TOV% 1位）。
  • ペイサーズはサンダーと比べて、相手にやや高いシュート効率とフリースローを許容している。

　小まとめ：両チームのスタッツから見える方向性

観点ペイサーズサンダー
得点効率◎（eFG%1位・TO少）○（安定性高）
守備効率△（中位）◎（DefRtg & Opp TOV% 1位）
試合展開トランジション重視（3位）より高速展開（2位）
攻撃の型シュート精度と判断力で勝負ボールロスがなく安定的

このように、ペイサーズは「精度とテンポ」で押し切るチーム、サンダーは「守備と安定」で勝ち切るチームといった対照的な構造がスタッツから浮かび上がります。

次章では、それぞれのチームがどのように“得点を作っているのか”、アシスト構造と得点分布に踏み込んで分析していきます。

🔀【　ペイサーズのオフェンス構造は、なぜ“分散型”なのか？　】

＜アシストネットワークと得点分布から見える主力と分散＞

　アシストネットワークとプレイヤーの役割分担

まずは下図のアシストネットワークと散布図（ASTPTS×FGPTS）をご覧ください。

※チャートの見方はこちら

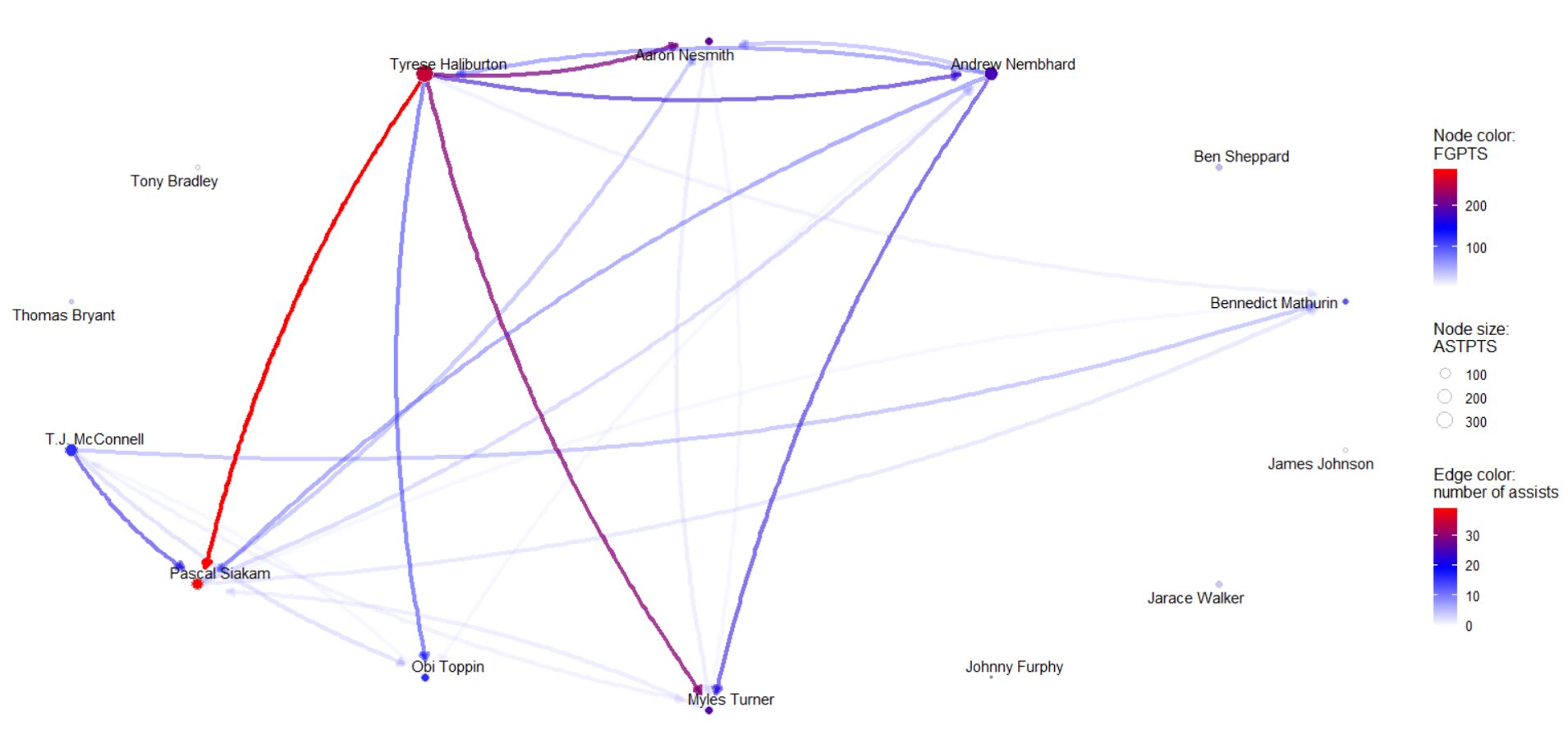
＜ ノードの色＝FGPTS（得点）、ノードサイズ＝ASTPTS（アシストにより生み出した得点）、線の太さ＝実際のアシスト本数） ＞

このネットワークから、以下のポイントが明確になります。

  • タイリース・ハリバートンがサイズの大きい赤色のノード、各プレイヤーに広がるエッジで描かれており、アシストと得点両面で攻撃の中核となっています。
  • パスカル・シアカムは特に得点面（FGPTSの赤色）で際立つノード。主力スコアラーであることが分かります。
  • アンドリュー・ネムハードはアシスト・得点の両面でハリバートンをサポート。ネットワークでも複数の太いエッジ（パス供給）が確認できます。

　ASTPTSとFGPTSの関係性（散布図）

※チャートの見方はこちら

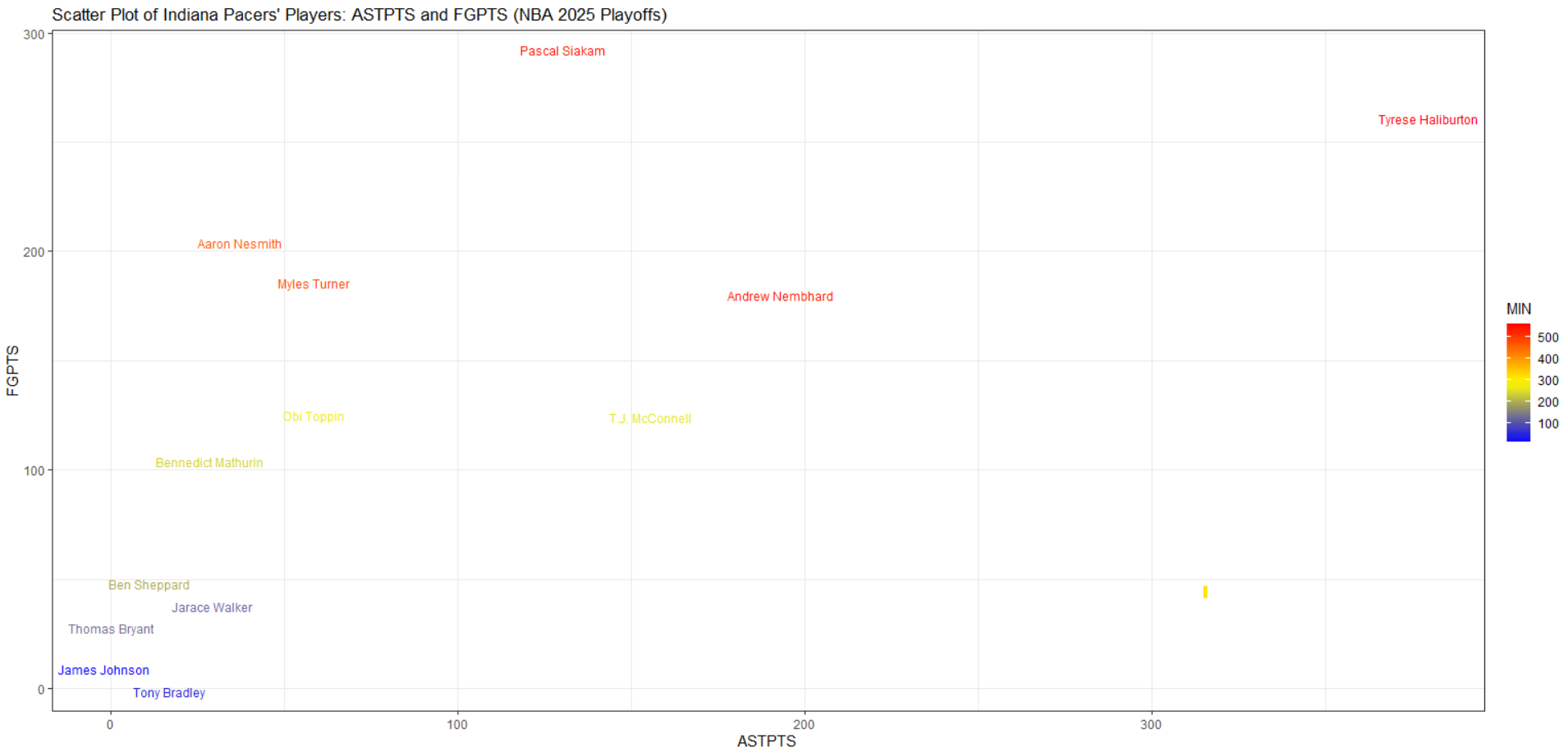
（横軸＝ASTPTS：アシストにより生み出した得点／縦軸＝FGPTS：実際のフィールドゴール得点、色は出場時間）

  • ハリバートンはASTPTSもFGPTSも高く、時間も最長レベル。“アシスト”と“得点”の両方の中心です。
  • シアカムはFGPTSが最大でASTPTSは中程度、得点面での主力。
  • ニスミス、ターナーがハリバートンとシアカムに続き、二次的なスコアラーとして安定した存在。
  • ネムハードはASTPTS・FGPTSともにバランスよく高水準で、サブクリエイター／サブスコアラーという役割が浮かび上がります。

　得点分布の“分散性”──ジニ係数と実際のスコアリング

ペイサーズの主力プレイヤーごとの総得点と1試合平均得点（NBA 2025 Playoffs）

プレイヤー試合数総得点1試合平均得点
パスカル・シアカム1633721.1
タイリース・ハリバートン1630118.8
マイルズ・ターナー1624315.2
アーロン・ニスミス1622514.1
アンドリュー・ネムハード1620512.8
ベネディクト・マサリン1515610.4
※ スタッツはNBA公式より参照。
  • プレーオフ1試合あたりの得点では、シアカム、ハリバートン、ターナー、ニスミス、ネムハード、マサリンの6人が二桁得点を記録。
  • 得点のジニ係数は20.62（PTS上位8名で算出）。
    この値はプレーオフ進出16チームの中で最も小さい。これはスコアリングの偏りが16チーム中、最も小さい（＝分散型）ことを意味します。（※ジニ係数は0から1（0～100%）の間の値をとり、スコアリングの偏りが全く無い場合は0、その偏りが大きくなるにつれて1に近づきます。ジニ係数の内容は過去記事を参照。）

　小まとめ：全員で得点する“分散型”オフェンス

観点内容
得点の分散性ジニ係数20.62（偏り最小）
主力シアカム（得点）、ハリバートン（アシスト＆得点）
サポートネスミス・ターナー・ネムハード（得点・アシストの両方で貢献）
体制6人が二桁得点＝「全員で取る」構造が完成

ペイサーズはハリバートン＆シアカムの2枚看板が主軸ですが、「全員で得点する」分散型オフェンスがプレーオフでも継続している──この事実は、ネットワーク図とジニ係数が裏付けています。

👥【　サンダーのオフェンス構造は、なぜ“役割分担型”なのか？　】

＜アシストネットワークと得点分布から見える役割集中と分担＞

　アシストネットワークと散布図から見る“二枚看板”と分担

まずは下図のアシストネットワークと散布図（ASTPTS×FGPTS）を確認します。

※チャートの見方はこちら

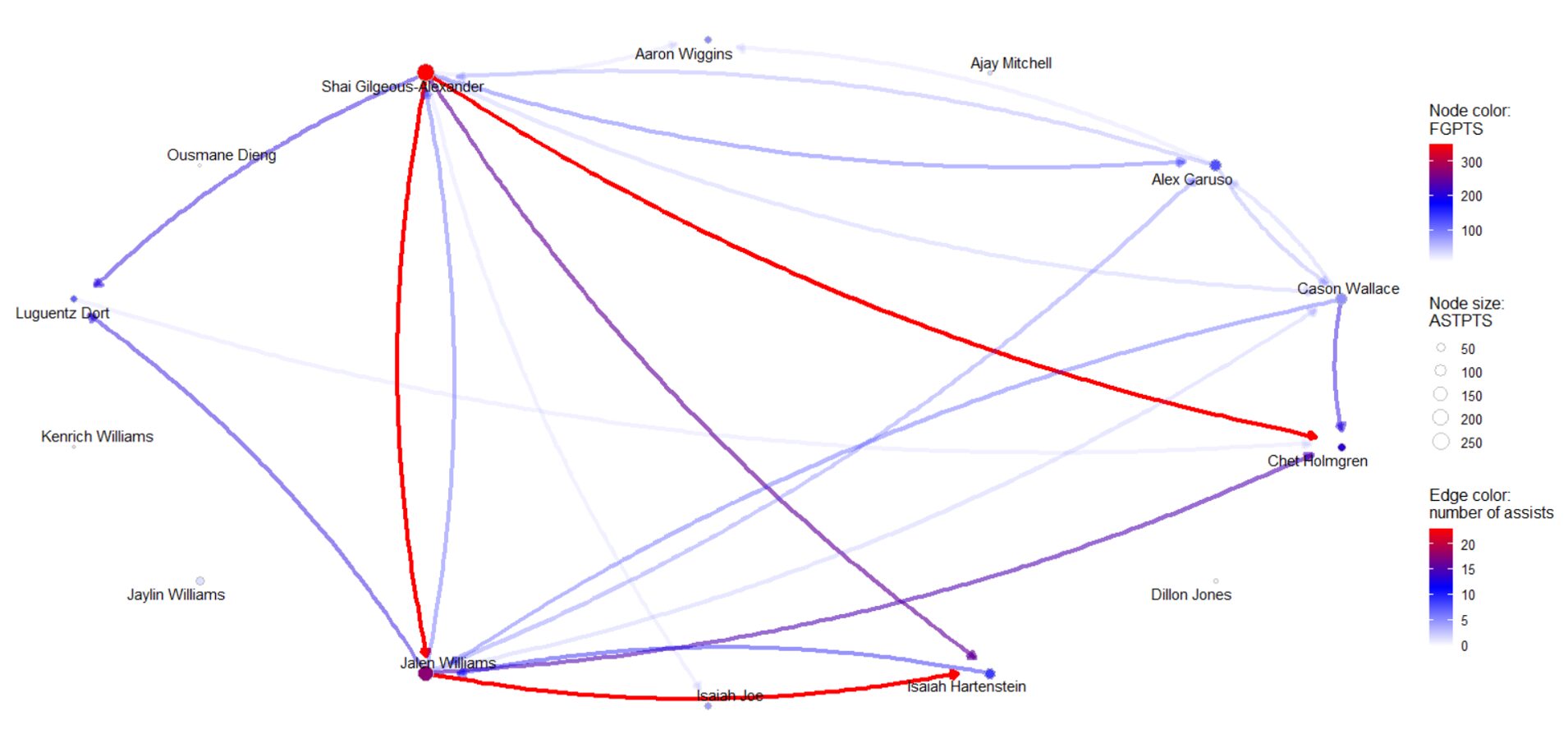
＜ ノードの色＝FGPTS（得点）、ノードサイズ＝ASTPTS（アシストにより生み出した得点）、線の太さ＝実際のアシスト本数） ＞

  • シェイ・ギルジャス＝アレキサンダー（SGA）がネットワークの中心。得点・アシストともに最大級。
  • ジェイレン・ウィリアムズがサブエース兼サブクリエイターとして機能。

　ASTPTSとFGPTSの関係性（散布図）

※チャートの見方はこちら

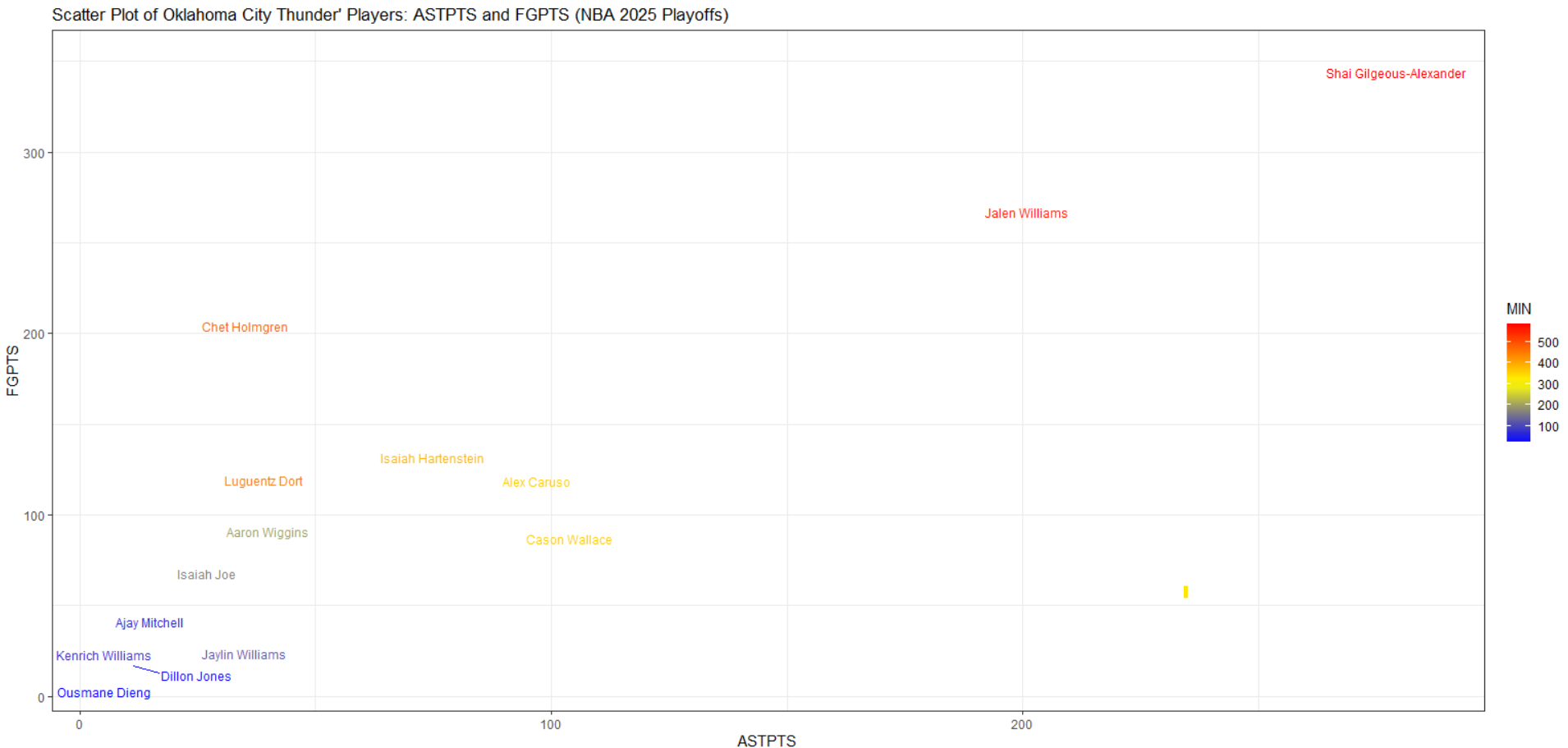
（横軸＝ASTPTS：アシストにより生み出した得点／縦軸＝FGPTS：実際のフィールドゴール得点、色は出場時間）

  • SGAがASTPTSもFGPTSも最大値で、攻撃の絶対的エース。
  • ジェイレン・ウィリアムズはやや控えめに見えますが、FGPTSはペイサーズのシアカムと同水準、ASTPTSはネムハード並み。十分な攻撃リーダーです。
  • チェット・ホルムグレンもFGPTSで200点程度を記録し存在感はあるが、他のメンバーに関しては攻撃面での存在感は限定的です。

　得点分布の集中度とジニ係数

サンダーの主力プレイヤーごとの総得点と1試合平均得点（NBA 2025 Playoffs）

プレイヤー試合数総得点1試合平均得点
シェイ・ギルジャス・アレクサンダー1647629.8
ジェイレン・ウィリアムズ1632720.4
チェット・ホルムグレン1626316.4
アイザイア・ハーテンシュタイン161479.2
アレックス・カルーソ161418.8
ルーゲンツ・ドート151257.8
※ スタッツはNBA公式より参照。
  • 1試合当たりの二桁得点はSGA、ジェイレン・ウィリアムズ、チェット・ホルムグレンの3名のみ。
  • 得点のジニ係数は37.35（上位8名で算出）。
    プレーオフ進出16チームの中では6番目に偏りが強く、明確な“スコア集中型”です。（※ジニ係数は0から1（0～100%）の間の値をとり、スコアリングの偏りが全く無い場合は0、その偏りが大きくなるにつれて1に近づきます。ジニ係数の内容は過去記事を参照。）

　役割集中の合理性──“守備型”メンバーの台頭

しかし、この偏りは単なる弱点ではありません。オフェンスにおける特定メンバーへの集中は、他のメンバーがディフェンスに専念できる構造の裏返しです。以下は、サンダーの主要プレイヤー（プレーオフ1試合当たりの出場時間が10分以上）の守備スタッツとプレーオフ平均をまとめた一覧表です。

サンダー主要プレイヤーの守備スタッツ一覧（NBA 2025 Playoffs）

PlayerMINDREBSTLBLKDEFRTG
シェイ・ギルジャス・アレクサンダー36.54.4 ↑1.6 ↑0.6 ↑102.5 ↑
ジェイレン・ウィリアムズ34.64.7 ↑1.6 ↑0.6 ↑105.4 ↑
チェット・ホルムグレン29.66.8 ↑0.8 2.0 ↑101.7 ↑
ルーゲンツ・ドート27.92.31.1 ↑0.4106.6 ↑
アイザイア・ハーテンシュタイン23.95.1 ↑0.8 0.6 ↑105.3 ↑
アレックス・カルーソ22.51.81.8 ↑0.499.6 ↑
ケイソン・ウォレス22.51.61.3 ↑0.497.9 ↑
アーロン・ウィギンズ13.51.60.40.3101.4 ↑
アイザイア・ジョー10.61.20.40.1107.2 ↑
プレーオフ平均–3.520.810.55113.07
※ スタッツはNBA公式より参照。平均値は出場時間10分以上の全てのプレイヤーで算出。太字↑は平均より上であることを示す。
  • SGAとジェイレン・ウィリアムズは攻守両面で主力。
  • チェットはリムプロテクト力が際立つ（DREB 6.8、BLK 2.0）。
  • ハーテンシュタインやカルーソ、ウォレスも守備面でリーグ平均を大きく上回る数値。

特にSTL（スティール）は主力ほとんどが平均超えで、そのジニ係数23.81。この値はプレーオフ進出16チームの中で4番目に小さく、これはスティールをするプレイヤーの偏りが小さい＝“全員でボールを奪う守備”がデータでも裏付けられています。（※ジニ係数は0から1（0～100%）の間の値をとり、スコアリングの偏りが全く無い場合は0、その偏りが大きくなるにつれて1に近づきます。ジニ係数の内容は過去記事を参照。）

　小まとめ：役割分担が生む“攻守両立型”チーム体制

観点内容
得点分布ジニ係数37.35（偏り大）
スコアリングSGA・ジェイレンの2枚看板
守備貢献役割分担型（攻撃では控えめな多くのプレイヤーがDREB・STL等で平均超え）
STLジニ係数23.81（偏りが小さい＝全員でスティール）

サンダーは「攻守の役割分担」を徹底し、攻撃はエース級の2人に、守備は全員でカバーする設計。この体制が、攻守ともにプレーオフ屈指の高パフォーマンスにつながっています。

両チームの“構造”は、どんな勝ち筋に繋がっているのか？

＜分散と集中、それぞれの効率のかたち＞

ここまで見てきたように、インディアナ・ペイサーズとオクラホマシティ・サンダーは、まったく異なるオフェンス構造でプレーオフを勝ち進んできました。しかし、その“分散”と“集中”のどちらが有利なのかは、一概に決めつけられません。両者はそれぞれに、チーム全体の効率と“勝ち筋”に直結する合理性を持っています。

　分散型（ペイサーズ）：多様性と耐性

ペイサーズの特徴は、誰か一人に依存しない「全員で得点する」分散型オフェンスです。

  • ジニ係数20.62（偏り最小）：上位6名が二桁得点
  • “誰でも得点できる”体制は、相手の守備対応を難しくし、マークを分散させやすい
  • ハリバートン離脱時にも、シアカムやネムハード、ニスミスが点を取る設計で不測の事態への耐性も高い

この多様性は、ケガや不調、相手ディフェンスの的確な対策に対しても崩れにくい“しぶとさ”につながります。

　集中型（サンダー）：エースの最大化と役割分担

一方、サンダーは明確な「二枚看板」の集中型オフェンスです。

  • ジニ係数37.35（偏り大）：得点源はSGA、ジェイレンの2人に集中
  • 他のメンバーは守備面やロールプレイに特化することで、チームディフェンスを全員で機能させる
  • オフェンスの効率はエース級の2人で押し上げ、ディフェンスは全員参加で底上げ

特にSGAとジェイレンは攻守両面の貢献度が高く、「攻撃はエース、守備は全員」の構図が強み。役割の明確さが、勝負どころでの集中力や“勝ち切る強さ”につながっています。

　“分散と集中”──二つの効率モデル

  • 分散型は「選択肢の多さ×柔軟性」で、シリーズを通じて大崩れしにくい
  • 集中型は「トップの爆発力×守備リソース集中」で、強敵相手にも強固な突破力を発揮

どちらも“チーム全体の最大効率”を突き詰めた設計であり、スタッツの違いは“思想の違い”そのものです。

　小まとめ

構造強み勝ち筋
分散型（ペイサーズ）多様性・耐性・柔軟性誰が抜けても形が崩れず、対応力で粘る
集中型（サンダー）役割分担・個の爆発力・守備全員型エースが引っ張り、守備で全員が締める

結局のところ、「分散」と「集中」のどちらが“正解”なのか──その答えは一つではありません。
どちらも現代NBAで勝ち切るための、極めて合理的な効率モデルだと言えるでしょう。

🔚【　おわりに　】

ここまで、インディアナ・ペイサーズとオクラホマシティ・サンダーのプレーオフにおけるオフェンス構造とチーム設計を、データとチャートをもとに比較してきました。

両チームのスタイルは対照的です。ペイサーズは「全員で点を取る」分散型、サンダーは「エースに集める」集中型。しかし、どちらもただの“形”ではなく、勝つための戦略と合理性が根底にあります。

  • ペイサーズは「誰でも得点できる」分散体制で、柔軟性と耐性が武器。
  • サンダーは「役割の明確な集中体制」で、エースと守備陣のメリハリが際立つ。

どちらが正解というよりも──“自分たちの強みを最大化した結果”としての構造が、データにはっきりと表れています。この違いが、NBAファイナルという極限の舞台でどんな勝負を生み出すか。ファンとしても、分析する側としても大いに注目したいポイントです。

最後に、「スタッツは勝ち方の“思想”そのもの」という視点を持って、今後も試合やチームを観ていくと、また違ったNBAの面白さが見えてくるはずです。

ここまで読んでいただきありがとうございました。
それでは、今回のトラッシュトークは以上です。

🏀【YouTube解説動画リンク】

  • 「全員で点を取るバスケ！ペイサーズの“均等性”をデータで徹底解説」をテーマに、この記事の内容をもとにした動画をYouTubeで公開しています。動画はこちら
  • 「攻撃はエース、守備は全員！サンダーの“集中型設計”をデータで徹底解説」をテーマに、この記事の内容をもとにした動画をYouTubeで公開しています。動画はこちら

🔗 【関連記事・シリーズ案内】

  • 【関連記事】「ペイサーズ vs ニックス：走力vsセカンドチャンス、データで可視化するニックスとペイサーズの“コア”のぶつかり合い」は、こちら
  • 【関連記事】「ペイサーズ vs キャバリアーズ：スタッツから読み解くチーム力の違いと逆転の糸口」は、こちら
  • 【関連記事】「サンダー vs ティンバーウルブズ：スティールとクラッチが交差する“攻防の構造”を読み解く」は、こちら
  • 【関連記事】「サンダー vs ナゲッツ：強固な守備と効率的オフェンスの激突」は、こちら
  • 【関連記事】「ジニ係数とは？：【ジニ係数を使って獲得点数とアシスト数のチーム内における偏りを数値化しよう】2022-23シーズンの獲得点数トップ4のキングス、ナゲッツ、ホークス、ブルズのラインナップに焦点をあてる」は、こちら

※参考＜統計ソフトRに入力するコマンド＞

統計ソフトRのインストール手順をまとめた記事も作成していますので、よろしければご参考ください。

library(BasketballAnalyzeR)
library(gridExtra)
library(dplyr)
Tbox2425 <- read.csv(file="Tbox_2425PO.csv")
Pbox2425 <- read.csv(file="Pbox_2425PO.csv")
dts.PbP.2425 <- read.csv(file="(10-22-2024)-(05-31-2025)-combined-stats.csv")
PbP2425 <- PbPmanipulation(dts.PbP.2425)

# Network of assists
PbP2425an <- subset(PbP2425, data_set=="NBA 2025 Playoffs" & team=="IND")
PbP2425AN <- PbP2425an[!(PbP2425an$event_type=="shot" & PbP2425an$result=="missed"),]
netdataAN <- assistnet(PbP2425AN)
plot(netdataAN, layout="circle", edge.thr=5, node.col="FGPTS", node.size="ASTPTS")
TABan <- netdataAN$assistTable
Xan <- netdataAN$nodeStats
names(Xan)[1] <- "Player"
dataAN <- merge(Xan, Pbox2425, by="Player")
dataANsp <- subset(dataAN, Team=="Indiana Pacers")
mypal <- colorRampPalette(c("blue", "yellow", "red"))
scatterplot(dataANsp, data.var=c("ASTPTS", "FGPTS"), z.var="MIN", labels=dataANsp$Player, palette=mypal, repel_labels=TRUE, title="Scatter Plot of Indiana Pacers' Players: ASTPTS and FGPTS (NBA 2025 Playoffs)")

PbP2425an <- subset(PbP2425, data_set=="NBA 2025 Playoffs" & team=="OKC")
PbP2425AN <- PbP2425an[!(PbP2425an$event_type=="shot" & PbP2425an$result=="missed"),]
netdataAN <- assistnet(PbP2425AN)
plot(netdataAN, layout="circle", edge.thr=5, node.col="FGPTS", node.size="ASTPTS")
TABan <- netdataAN$assistTable
Xan <- netdataAN$nodeStats
names(Xan)[1] <- "Player"
dataAN <- merge(Xan, Pbox2425, by="Player")
dataANsp <- subset(dataAN, Team=="Oklahoma City Thunder")
mypal <- colorRampPalette(c("blue", "yellow", "red"))
scatterplot(dataANsp, data.var=c("ASTPTS", "FGPTS"), z.var="MIN", labels=dataANsp$Player, palette=mypal, repel_labels=TRUE, title="Scatter 

# Gini index with respect to PTS, AST, STL
no.teams <- nrow(Tbox2425)
GINI_PTS <- array(0, no.teams)
for (k in 1:no.teams) { 
       Teamk <- Tbox2425$Team[k] 
       Pbox2425.sel <- subset(Pbox2425, Team==Teamk) 
       index1 <- inequality(Pbox2425.sel$PTS, npl=8) 
       GINI_PTS[k] <- index1$Gini
       }

GINI_AST <- array(0, no.teams)
for (k in 1:no.teams) { 
       Teamk <- Tbox2425$Team[k] 
       Pbox2425.sel <- subset(Pbox2425, Team==Teamk) 
       index2 <- inequality(Pbox2425.sel$AST, npl=8) 
       GINI_AST[k] <- index2$Gini
       }

GINI_STL <- array(0, no.teams)
for (k in 1:no.teams) { 
       Teamk <- Tbox2425$Team[k] 
       Pbox2425.sel <- subset(Pbox2425, Team==Teamk) 
       index3 <- inequality(Pbox2425.sel$STL, npl=8) 
       GINI_STL[k] <- index3$Gini
       }

dts <- data.frame(Team=Tbox2425$Team, GINI_PTS, GINI_AST, GINI_STL, PTS=Tbox2425$PTS, AST=Tbox2425$AST, STL=Tbox2425$STL)
スポンサーリンク
スポンサーリンク
スポンサーリンク
** データ分析を実践する際に参考にしている書籍です **

Paola Zuccolotto and Marica Manisera (2020), Basketball Data Science – with Applications in R. Chapman and Hall/CRC. ISBN 9781138600799.

2024-25シーズン2025 NBAプレーオフスタッツ分析
ジニ係数ネットワーク分析散布図

ご感想などありましたら、X（旧Twitter）[@basketrashtalk](https://x.com/basketrashtalk)までお気軽にどうぞ！
このブログの内容をもとにした動画もYouTubeにて公開中です。
こちらのチャンネルからご覧いただけます → Trash Talk｜バスケ分析 by Kaneshiro

シェアする
Kaneshiroをフォローする
Kaneshiro
タイトルとURLをコピーしました