今回は、レーティングやFour Factorsなどのスタッツを使って、クラスター分析によるNBAチームのグループ分けを実行していきます。
使用する統計ソフトはR、データは2022-23レギュラーシーズンのTboxとObox(過去記事参照)を使用します。
まずは、今回のクラスター分析で使用する変数の内容から確認していきます。
※データ分析を実践する際に参考にしている書籍『Basketball Data Science: With Applications in R』の紹介記事も書きましたので、よろしければご確認ください。
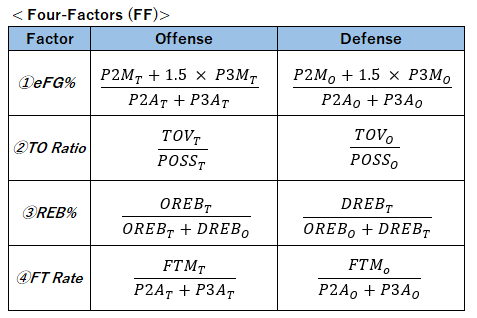
分析に使用する変数<ORtg、DRtg、Four Factorsがベース>
まずは、今回のクラスター分析で使用する変数の説明をしていきます。
参考書籍としている“Paola Zuccolotto and Marica Manisera (2020), Basketball Data Science – with Applications in R.(以下、P. Zuccolotto and M. Manisera (2020)と表記します。)”の内容に沿って、下記の7つの変数を使用して分析を進めていきます。
- ① OD.Rtg = ORtg / DRtg
ディフェンスレーティングに対するオフェンスレーティングの比率 - ② F1.r = eFG%.Offense / eFG%.Defense
対戦チームのeFG%に対する自チームのeFG%の比率 - ③ F2.r = TO Ratio. Defense / TO Ratio. Offense
自チームのTO Ratioに対する対戦チームのTO Ratioの比率 - ④ F3.Off:REB%. Offense
オフェンスリバウンドに関する REB% - ⑤ F3.Def:REB%. Defense
ディフェンスリバウンドに関する REB% - ⑥ P3M:3Pシュート成功数
- ⑦ STL.r = STLt / STLo
対戦チームのスティール数に対する自チームのスティール数の比率
上記①~⑤の変数のベースとなっているレーティングやFour Factorsについては、下記の記事で紹介していますので、よろしければご参考ください。
また、クラスター分析を実行する際には、上記の変数に関してはすべて標準化の処理が行われます。
標準化の処理を変数に施して分析を進めた過去記事もありますので、よろしければ下記もあわせてご参考ください。
なお、上記の変数を算出するコマンドは下記のとおりです。
> library(BasketballAnalyzeR) #パッケージBasketballAnalyzeRの読み込み
> Tbox2223 <- read.csv(file="Tbox_2223.csv") # Tbox2223の読み込み
> Obox2223 <- read.csv(file="Obox_2223.csv") # Obox2223の読み込み
> FF2223 <- fourfactors(Tbox2223, Obox2223) #fourfactors関数でPACE、ORtg、Four Factorsを算出
> OD.Rtg <- FF2223$ORtg/FF2223$DRtg
> F1.r <- FF2223$F1.Off/FF2223$F1.Def
> F2.r <- FF2223$F2.Def/FF2223$F2.Off
> F3.Off <- FF2223$F3.Off
> F3.Def <- FF2223$F3.Def
> P3M <- Tbox2223$P3M
> STL.r <- Tbox2223$STL/Obox2223$STL
> data2223 <- data.frame(OD.Rtg, F1.r, F2.r, F3.Off, F3.Def, P3M, STL.r) #data.frame()を使って7変数をまとめてdata2223へ格納続いて、クラスター分析を実行する前に、クラスター数の検討を行いたいと思います。
K-means法による非階層的クラスター分析に伴うクラスター数の検討
今回は、K-means法による非階層的クラスター分析を行うため、事前にクラスター数を検討する必要があります。
ここでは、参考書籍としているP. Zuccolotto and M. Manisera (2020)に基づいて、以下の算式BD/TDを用いてクラスター数の検討を行っていきます。
BD/TD
\(TD=\sum ^{k}_{h=1}\sum ^{n_{h}}_{i=1}\left( x_{ih}-\mu \right) ^{2}\), \(BD=\sum ^{k}_{h=1}\left( \mu _{h}-\mu \right) ^{2}n_{h}\), \(WD=\sum ^{k}_{h=1}\sigma _{h}^{2}n_{h}\),
Paola Zuccolotto and Marica Manisera (2020), Basketball Data Science – with Applications in R. Chapman and Hall/CRC. ISBN 9781138600799.
TD=BD+WD
\(x_{ih}\)は\(h\)番目のクラスター内の\(i\)番目のデータ、\(μ\)は全データの平均、\(n_{h}\)は\(h\)番目のクラスターに属するデータ数、\(μ_{h}\)は\(h\)番目のクラスターに属するデータのみで算出した平均、\(\sigma _{h}^{2}\)は\(h\)番目のクラスター内の分散を表します。
上記の算式BD/TDは、「分析対象データの偏差の総和」に占める「各クラスター間の偏差の総和」の割合を示しており、BDの値が大きければ、データ全体のばらつきのうち各クラスター間のばらつきで説明できる度合いが強いと解釈することが出来ます。
また、分析対象データから算出されるTDの値は一定であり、かつ、上記の関係式TD=BD+WDより、BDの値が大きくなればWD(各クラスター内の偏差の総和)の値が小さくなることが分かります。
このことから、各クラスター間の異質性が高くなれば、各クラスター内の異質性が低く(同質性が高く)なると考えられ、その結果として算出されるBD/TDを用いて、分析対象データに対する分類の当てはまりの良さを判断することが可能になります。
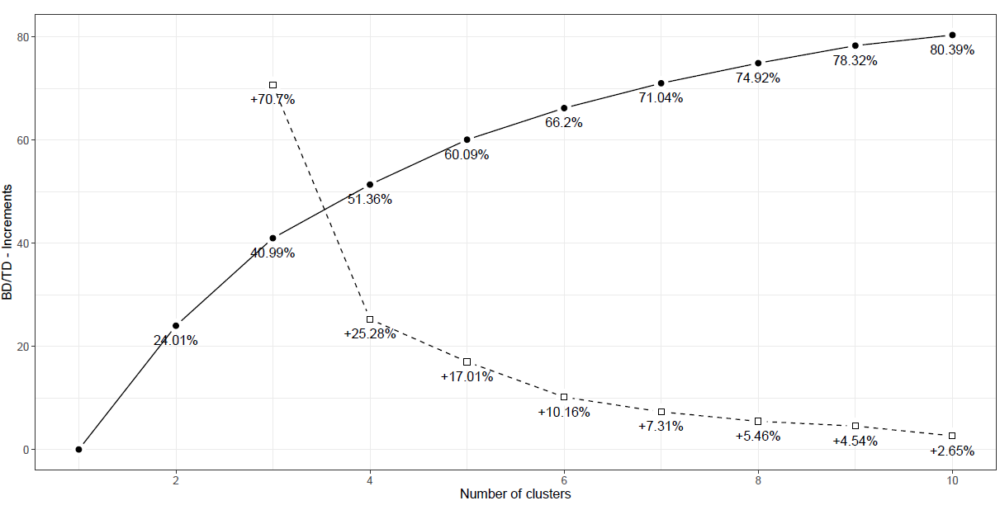
なお、今回のデータを使って実際に算出したBD/TDのグラフは、下記のとおりです。
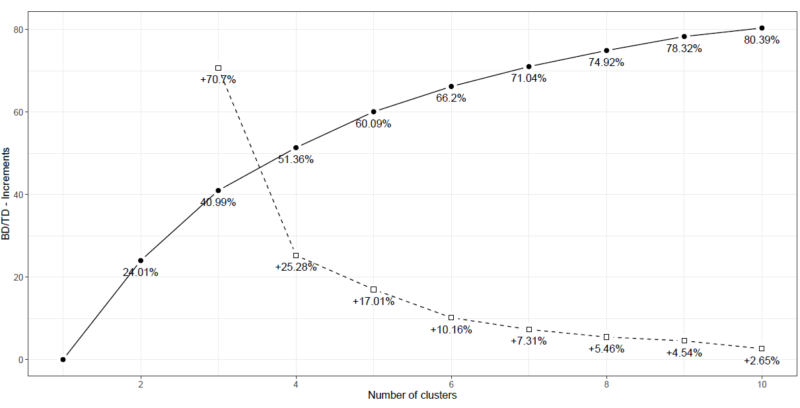
横軸はクラスター数を表し、実線のグラフは各クラスター数におけるBD/TDの値の推移を示しています。(例えば、クラスター数が2の場合のBD/TDは、約24.01%となります。)
破線のグラフは、クラスター数を1つ増やした時のBD/TDの増加率の推移を示しています。(例えば、クラスター数を2→3に増やした時、BD/TDは約70.7%増加することになります。)
P. Zuccolotto and M. Manisera (2020)では、BD/TDの値は50%よりも高いことが望ましく、BD/TDの増加率に関しては、分析対象のデータ数が少ない(30チーム)ことを考慮して、10%よりも大きい増分となることが望ましいとしています。
上記の判断基準に従い今回作成したグラフを確認すると、クラスター数を4→5に増やした時のBD/TDの増加率が約17.01%、クラスター数が5の場合のBD/TDの値が約60.9%であることから、今回はクラスター数を5に設定して分析を進めていきます。
なお、上記のグラフを出力するコマンドは下記のとおりです。
> set.seed(29) #再現性のためset.seed()を設定
> kclu1 <- kclustering(data2223) #kclustering()を使ってBD/TDを算出しkclu1へ格納
> plot(kclu1) #plot()を使ってグラフを出力続いて、クラスター分析によるチームの分類を示していきます。
クラスター分析の実行<セルティックス、ウォリアーズ、バックスはフィールドショットに強みを持つ>
クラスター分析を実行した結果は、下記のとおりです。
ClusterList (2022-23 Regular Season)
[1]
"Atlanta Hawks" "Chicago Bulls" "Cleveland Cavaliers"
"Denver Nuggets" "Memphis Grizzlies" "Miami Heat"
"New Orleans Pelicans" "New York Knicks" "Orlando Magic"
"Philadelphia 76ers" "Phoenix Suns" "Sacramento Kings"
------------------------------------------------------------------------------------------
[2]
"Boston Celtics" "Golden State Warriors" "Milwaukee Bucks"
------------------------------------------------------------------------------------------
[3]
"Oklahoma City Thunder" "Toronto Raptors"
------------------------------------------------------------------------------------------
[4]
"Charlotte Hornets" "Detroit Pistons" "Houston Rockets"
"San Antonio Spurs"
------------------------------------------------------------------------------------------
[5]
"Brooklyn Nets" "Dallas Mavericks" "Indiana Pacers"
"LA Clippers" "Los Angeles Lakers" "Minnesota Timberwolves"
"Portland Trail Blazers" "Utah Jazz" "Washington Wizards"上記では、前述した2022-23レギュラーシーズンにおける7変数に応じて、NBA全30チームが5つのクラスターに分類されています。
上記の分類の解釈をしやすくするために、クラスターごとの7変数の平均値をレーダーチャートを用いて下記に示します。
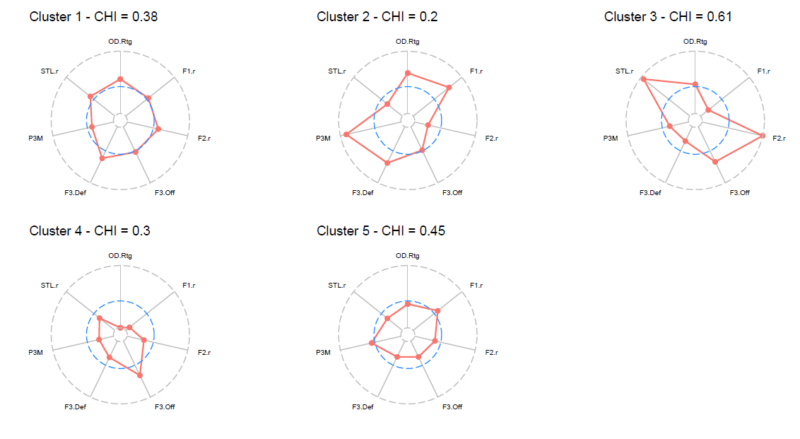
レーダーチャート内にある青色の破線は、NBA全30チームの平均値(前述のとおり標準化の処理がされているため平均0)を表しています。
なお、レーダーチャート内に示されているCHIの数値は、クラスターごとの変数の分散の平均値を表しており、下記の算式により算出されます。
$$CHI _{h}=\dfrac{\sum ^{p}_{j=1}\sigma _{jh}^{2}}{p}$$
Paola Zuccolotto and Marica Manisera (2020), Basketball Data Science – with Applications in R. Chapman and Hall/CRC. ISBN 9781138600799.
\(p\)は変数の数(今回の場合は7)、\(\sigma _{jh}^{2}\)は\(h\)番目のクラスター内の\(j\)番目の変数の分散を表しており、P. Zuccolotto and M. Manisera (2020)では、CHIの数値が50%以下となっていることが望ましいとしています。
上記のレーダーチャートを考慮すると、それぞれのクラスターについては以下の特徴を読み取ることが出来ます。(※クラスター3に関してはCHIの値が50%を超えているため、今回の結果については参考値扱いとして進めていきます。)
- クラスター1:3Pシュート成功数を除く各スタッツにおいて、平均以上の水準を満たしているチーム。(全12チーム)
- クラスター2:フィールドゴール成功率が高く、特に3Pシュートに強みを持つチームであるため、オフェンスの効率が良い。また、ディフェンスリバウンドも強いチーム。(全3チーム)
- クラスター3:ターンオーバーに有利性を持ち、対戦相手と比較して相対的にスティール数が多いチーム。(全2チーム、CHIが50%を超えるため参考値扱い。)
- クラスター4:オフェンスリバウンド数を除く各スタッツにおいて、平均水準を大きく下回るチーム。オフェンスリバウンドに関しては、フィールドゴール成功率が低いことによりオフェンスリバウンドの機会が増え、その結果として高水準になっているとも考えられる。(全4チーム)
- クラスター5:フィールドゴール成功率と3Pシュート成功数は平均並みの水準だが、それら以外の各スタッツが平均以下の水準となっているチーム。(全9チーム)
なお、上記のクラスター分析を実行するコマンドは、下記のとおりです。
> set.seed(29) #再現性のためset.seed()を設定
> kclu2 <- kclustering(data2223, labels=Tbox2223$Team, k=5) #kclustering()を使ってクラスター分析を実行しkclu2へ格納
> plot(kclu2) #plot()を使ってレーダーチャートを出力次回について
今回は、K-means法による非階層的クラスター分析を用いて、2022-23レギュラーシーズンにおけるNBA全30チームのグループ分けを行いました。
グループ分けの際には、使用した7つの変数を考慮することで、各チームが属するそれぞれのクラスターのおおまかな特徴を把握することが出来ました。
次回記事は今回の結果を踏まえて、プレーオフ進出の情報や得失点数などを交えた分析を進めていきたいと思います。
なお、本記事は、記事の最後に紹介している書籍を参考にして作成しています。
それでは、今回のトラッシュトークは以上です。
【参考書籍】
Paola Zuccolotto and Marica Manisera (2020), Basketball Data Science – with Applications in R. Chapman and Hall/CRC. ISBN 9781138600799.
※本書籍の紹介記事を書いていますので、よろしければご参考ください。
川端一光、岩間徳兼、鈴木雅之(2018)『Rによる多変量解析入門ーデータ分析の実践と理論ー』オーム社.
【参考ウェブサイト】
統計WEB.“7-6. 非階層型クラスター分析”.統計学の時間.https://bellcurve.jp/statistics/course/27301.html,(参照2023-11-25).