今回は、ミルウォーキー・バックスのフィールドゴールに関する情報を使って、クラスター分析によるフィールドゴールのグループ分けを実行していきます。
使用する統計ソフトはR、データは2022-23シーズンのPbP. BDB(過去記事参照)を使用します。
まずは、今回のクラスター分析で使用する変数の内容から確認していきます。
※データ分析を実践する際に参考にしている書籍『Basketball Data Science: With Applications in R』の紹介記事も書きましたので、よろしければご確認ください。
分析に使用する変数<バックスのPTS、FGの距離、クォーター経過時間、playlength>
今回のクラスター分析では、下記の4つの変数を使用します。
- PTS:フィールドゴールに対する得点(”0”、”2”、”3”のいずれかの値をとる。)
- DIS:フィールドゴールのリングからの距離
- TIMEQ:フィールドゴールを放った時点におけるクォーターの経過時間
- PL(playlength):プレイヤーがシュートを放った場合に、そのシュートの直前のイベントからそのシュートを放つまでの間に何秒経過していたのかを表す項目。例えば、リバウンドを獲得(直前のイベント)した後、その5秒経過後にシュートを放ったのであればplaylengthは”5”となる。
上記の4変数に関してクラスター分析を実行する際には、すべて標準化の処理が行われます。
標準化の処理を変数に施して分析を進めた過去記事もありますので、よろしければ下記もあわせてご参考ください。
なお、上記の変数を作成するコマンドは下記のとおりです。
> library(BasketballAnalyzeR) #パッケージBasketballAnalyzeRの読み込み
> dts.PbP.2223 <- read.csv(file="PbP. BDB_2223.csv") # PbP. BDB2223の読み込み
> PbP2223 <- PbPmanipulation(dts.PbP.2223) # PbPmanipulation関数でPbP2223を作成
> shotsMIL <- subset(PbP2223, !is.na(PbP2223$shot_distance) & PbP2223$team=="MIL")
> shotsMIL <- dplyr::mutate_if(shotsMIL, is.factor, droplevels)
> attach(shotsMIL)
> data2223 <- data.frame(PTS=points, DIST=shot_distance, TIMEQ=periodTime, PL=playlength)
> detach(shotsMIL)続いて、クラスター分析を実行する前に、クラスター数の検討を行いたいと思います。
K-means法による非階層的クラスター分析に伴うクラスター数の検討
本記事ではK-means法による非階層的クラスター分析を行うため、次はクラスター数を事前に検討していきます。
なお、クラスター数の検討に使用する指標“BD/TD”については、下記の過去記事で紹介していますので、よろしければご参考ください。
前述した4変数を使って算出したBD/TDのグラフは、下記のようになります。
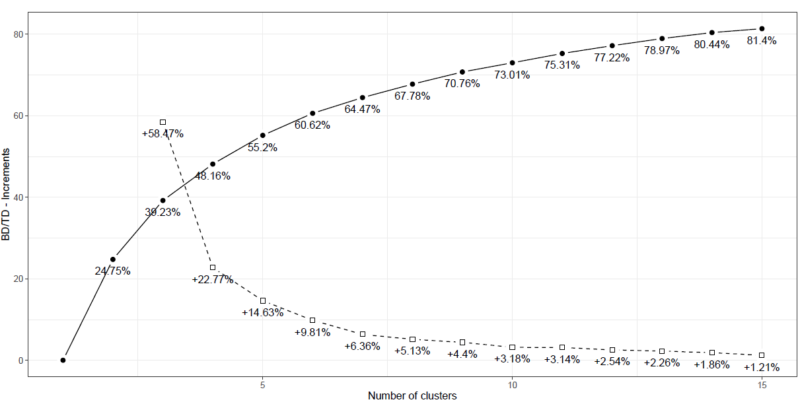
横軸はクラスター数を表し、実線のグラフは各クラスター数におけるBD/TDの値の推移を示しています。(例えば、クラスター数が2の場合のBD/TDは、約24.75%となります。)
破線のグラフは、クラスター数を1つ増やした時のBD/TDの増加率の推移を示しています。(例えば、クラスター数を2→3に増やした時、BD/TDは約58.47%増加することになります。)
参考書籍としている“Paola Zuccolotto and Marica Manisera (2020), Basketball Data Science – with Applications in R.(以下、P. Zuccolotto and M. Manisera (2020)と表記します。)”では、BD/TDの値は50%よりも高いことが望ましく、BD/TDの増加率に関しては、分析対象のデータ数にもよりますが、5%~10%よりも大きい増分となることが望ましいとしています。
上記の判断基準を考慮しながら今回作成したグラフを確認すると、クラスター数を5→6に増やした時のBD/TDの増加率が約9.81%、クラスター数が6の場合のBD/TDの値が約60.62%であることから、今回はクラスター数を6に設定して分析を進めていきます。
なお、上記のグラフを出力するコマンドは下記のとおりです。
> set.seed(1) #再現性のためset.seed()を設定
> kclu1 <- kclustering(data2223, algorithm="MacQueen", nclumax=15, iter.max=500)
> plot(kclu1)続いて、バックスの2022-23シーズンにおけるフィールドゴールについて、クラスター分析による分類を実行していきます。
クラスター分析によるバックスのフィールドゴールの分類<NBA2022-23シーズン>
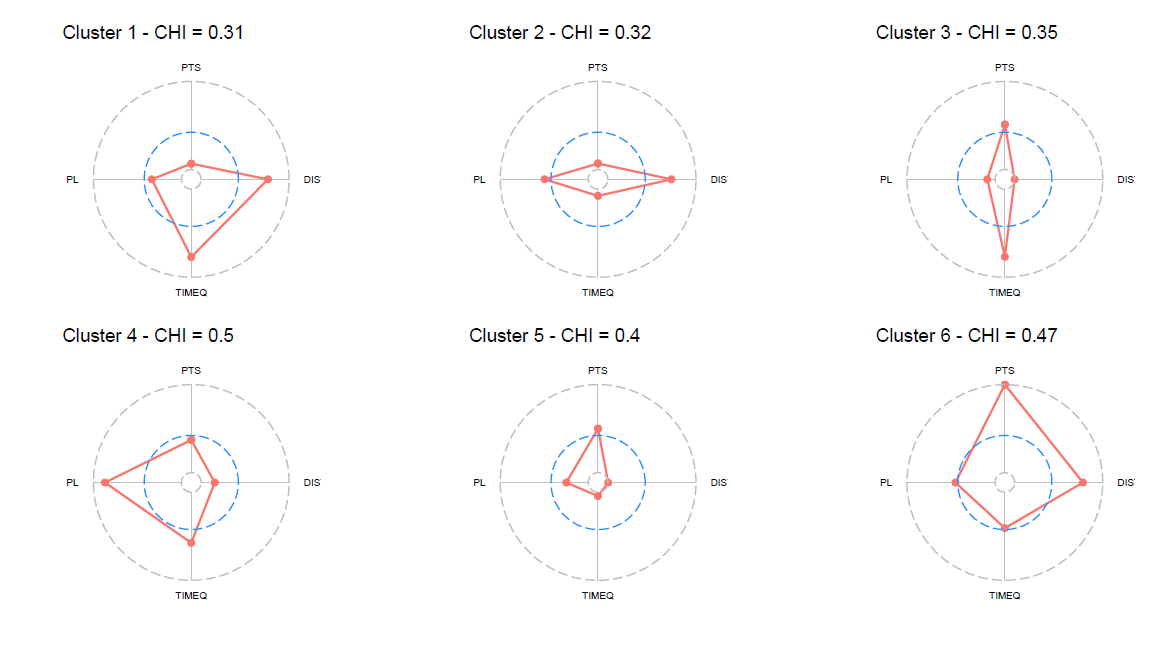
バックスのフィールドゴールに関して6つのクラスターに分類した上で、各クラスターにつき前述した4変数の平均値をレーダーチャートで示すと、下記のようになります。

レーダーチャート内にある青色の破線は、2022-23シーズンにおけるバックスの各変数の平均値(前述のとおり標準化の処理がされているため平均0)を表しています。
なお、上記のレーダーチャート内で示されているCHIの数値に関しては、下記の過去記事で紹介していますので、よろしければご参考ください。
参考書籍であるP. Zuccolotto and M. Manisera (2020)では、CHIの数値が50%以下となっていることが望ましいとされており、上記のレーダーチャート内のCHIの数値を確認すると、すべてのクラスターでその数値が50%以下となっていることがわかります。
クラスター分析によるフィールドゴールの分類の解釈をしやすくするために、下記に各クラスターに属するフィールドゴールのショットチャートも併せて示します。
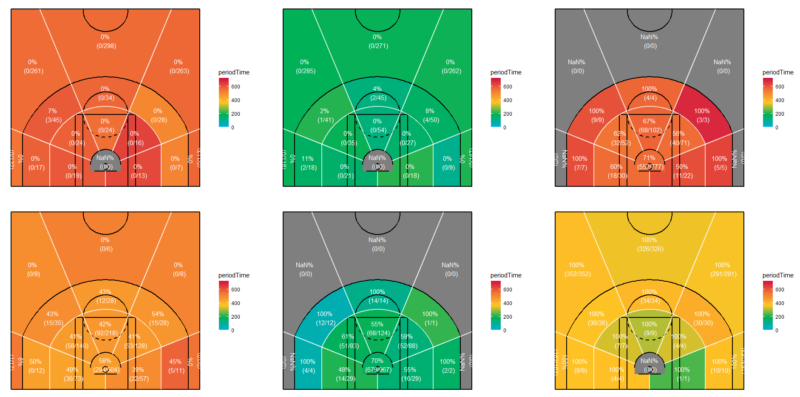
上記のショットチャートに関して、上段は左から順番にクラスター1、クラスター2、クラスター3のショットチャートが示され、下段は左から順番にクラスター4、クラスター5、クラスター6のショットチャートが示されています。
上記のショットチャートでは、コートが16のエリアに分割され、各エリアはフィールドゴールを放った時点におけるクォーターの経過時間(periodTime)の平均値で色分けされています。(水色はクォーターの序盤、黄色はクォーターの中盤、赤色はクォーターの終盤であることを表しています。)
なお、%表記されている数値はそのエリア内のフィールドゴール成功率を表し、その下の()書きは(フィールドゴール成功数/フィールドゴール試投数)を示しています。
上記のレーダーチャートとショットチャートを考慮すると、バックスのフィールドゴールに関する6つのクラスターについては、下記のような特徴を読み取ることが出来ます。
- クラスター1:クォーターの終盤で失敗したフィールドゴール(ノーチャージセミサークルエリア内を除く)で、その構成は主に3Pシュートが中心となる。playlengthの水準が平均をやや下回ることから、やや早い展開で試投したフィールドゴールが属する。
- クラスター2:クォーターの序盤で失敗したフィールドゴール(ノーチャージセミサークルエリア内を除く)で、その構成は主に3Pシュートが中心となる。playlengthの水準が平均をやや上回ることから、やや遅い展開で試投したフィールドゴールが属する。
- クラスター3:クォーターの終盤で試投したフィールドゴール(3Pシュートを除く)で、その構成は主にペイントエリア内とその周辺からのフィールドゴールが中心となる。Playlengthの水準が最も低いことから、早い展開で試投したフィールドゴールが属する。
- クラスター4:クォーターの中盤で試投したフィールドゴールで、その構成は主にペイントエリア内とその周辺からのフィールドゴールが中心となる。playlengthの水準が最も高いことから、遅い展開で試投したフィールドゴールが属する。
- クラスター5:クォーターの序盤で試投したフィールドゴール(3Pシュートを除く)で、その構成は主にペイントエリア内とその周辺からのフィールドゴールが中心となる。playlengthの水準が平均を下回ることから、比較的早い展開で試投したフィールドゴールが属する。
- クラスター6:クォーターの中盤で成功したフィールドゴール(ノーチャージセミサークルエリア内を除く)で、その構成は主に3Pシュートが中心となる。playlengthの水準が平均的であることから、チームの標準的なテンポで試投したフィールドゴールが属する。
なお、上記のレーダーチャートとショットチャートを出力するコマンドは、下記のとおりです。
> set.seed(1)
> kclu2 <- kclustering(data2223, algorithm="MacQueen", iter.max=500, k=6)
> plot(kclu2) #plot()を使ってレーダーチャートを出力
> cluster <- as.factor(kclu2$Subjects$Cluster)
> shotsMIL <- data.frame(shotsMIL, cluster)
> shotsMIL$xx <- shotsMIL$original_x/10
> shotsMIL$yy <- shotsMIL$original_y/10 - 41.75
> no.clu <- 6
> p1 <- p2 <- vector(no.clu, mode="list")
> for (k in 1:no.clu) {
+ shotsMIL.k <- subset(shotsMIL,cluster==k)
+ p1[[k]] <- shotchart(data=shotsMIL.k, x="xx", y="yy",
+ z="result", type=NULL,
+ scatter = TRUE,
+ drop.levels=FALSE)
+ p2[[k]] <- shotchart(data=shotsMIL.k, x="xx", y="yy",
+ z="periodTime",
+ col.limits=c(0,720),
+ result="result", num.sect=5,
+ type="sectors", scatter=FALSE)
+ }
> library(gridExtra)
> grid.arrange(grobs=p2, nrow=2) #grid.arrange()を使ってショットチャートを2行3列で出力次回について
今回は、K-means法による非階層的クラスター分析を用いて、2022-23シーズンにおけるバックスのフィールドゴールのグループ分けを行いました。
グループ分けの際には、今回使用した4変数を考慮し、さらに各クラスターに属するフィールドゴールのショットチャートを参照することで、6つのクラスターのおおまかな特徴を把握することが出来ました。
次回記事は今回の結果を踏まえた上で、各プレイヤーが試投したフィールドゴールがどのクラスターに属するかを確認し、クラスター内におけるプレイヤー別のフィールドゴール試投数の偏りに関して分析を進めていきたいと思います。
なお、本記事は、記事の最後に紹介している書籍を参考にして作成しています。
それでは、今回のトラッシュトークは以上です。
【参考書籍】
Paola Zuccolotto and Marica Manisera (2020), Basketball Data Science – with Applications in R. Chapman and Hall/CRC. ISBN 9781138600799.
※本書籍の紹介記事を書いていますので、よろしければご参考ください。