今回は、Play By Playデータを使って、統計ソフトRによるアシストのネットワーク分析について紹介していきたいと思います。
データは、2022-23シーズンのPbP. BDB(過去記事参照)を使用し、チームはデンバー・ナゲッツに焦点をあてていきます。
まずは、2022-23シーズンにおけるナゲッツのアシストネットワークのグラフから作成していきます。
※データ分析を実践する際に参考にしている書籍『Basketball Data Science: With Applications in R』の紹介記事も書きましたので、よろしければご確認ください。
デンバー・ナゲッツのアシストネットワーク<アシストの中心的プレイヤーはヨキッチ>
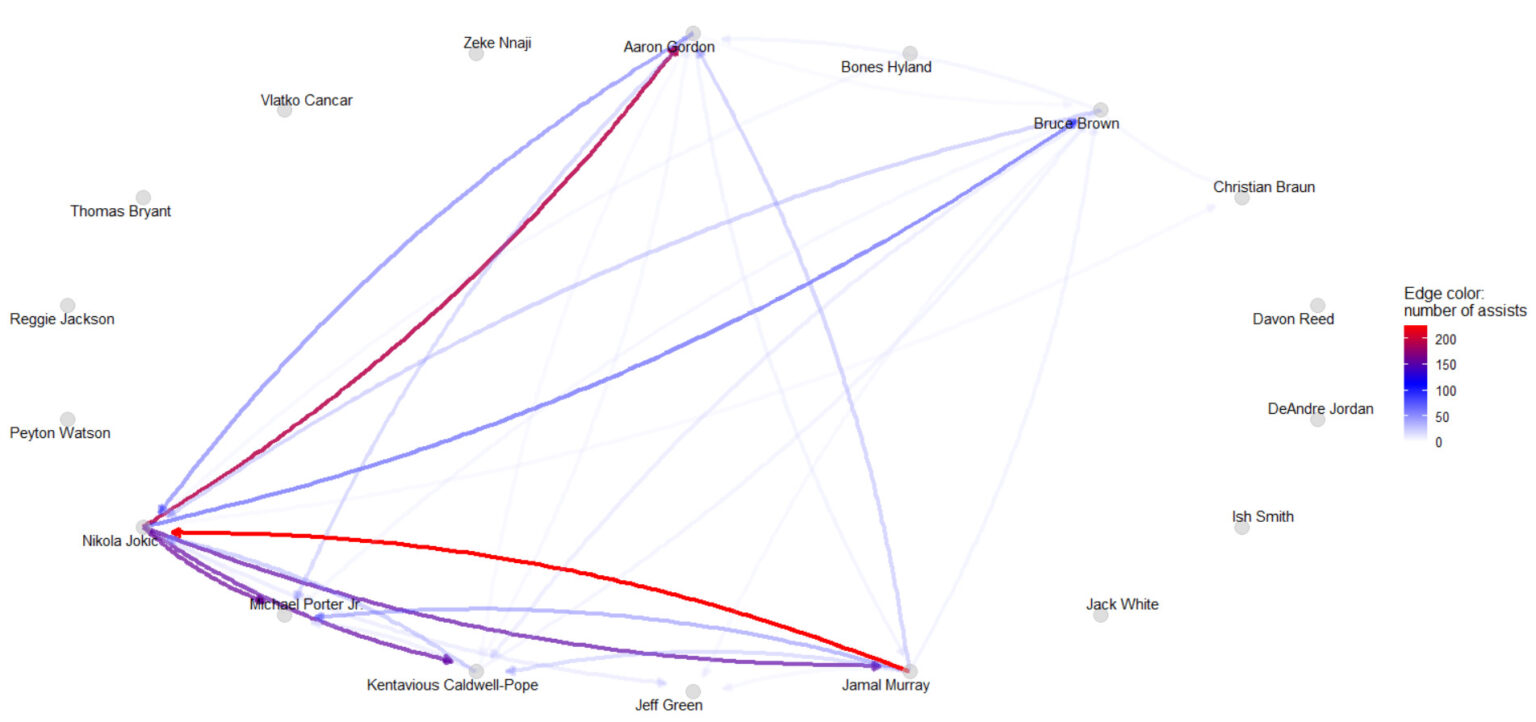
2022-23シーズンにおけるナゲッツのアシストネットワークのグラフは、下記のとおりです。
上記のグラフでは、ノードは各プレイヤーを表し、エッジは方向性があるため矢印で表現されています。
各プレイヤーはエッジである矢印で結ばれており、エッジの起点となっているプレイヤーはアシストを出した側、エッジの終点となっているプレイヤーはアシストを受けた側であることを表しています。
エッジの色はアシストの本数と対応しており、アシスト数が多ければ赤色を示し、アシスト数が少なければ薄紫色へと変化していきます。
なお、上記のグラフではネットワークの状況を見やすくするために、アシスト数20以下となるエッジの表記を省略しています。
上記のグラフを確認すると、ナゲッツのアシストネットワークは主にニコラ・ヨキッチ、アーロン・ゴードン、ブルース・ブラウン、ジャマール・マレー、K.コールドウェル・ポープ、マイケル・ポーターJr.の6人で構成されていることが分かります。
エッジの起点とその方向に目を向けると、チーム内のアシストにおいてはヨキッチが重要な役割を担っていることが読み取れます。
ヨキッチから供給されるアシストについては、ゴードンへのアシストが若干多くはなっていますが、おおむね同程度のアシストがバランス良く5人へ供給されていることが分かります。
ヨキッチほどではないにしても、マレーのほうもアシストの供給源になっていることが読み取れますが、その多くはヨキッチへのアシストに偏っています。
ナゲッツに関してはチームの特徴の1つとして、ガードのマレーではなく、センターのヨキッチがアシスト面で重要な役割を果たしている点を挙げることができます。
それでは、ヨキッチが試合に出場していない場合、ナゲッツのアシストネットワークはどのように変化するでしょうか。
ヨキッチがコート上にいない場合、ナゲッツのアシストネットワークのグラフは下記のようになります。(※下記グラフでは、アシスト数10以下となるエッジの表記を省略しています。)
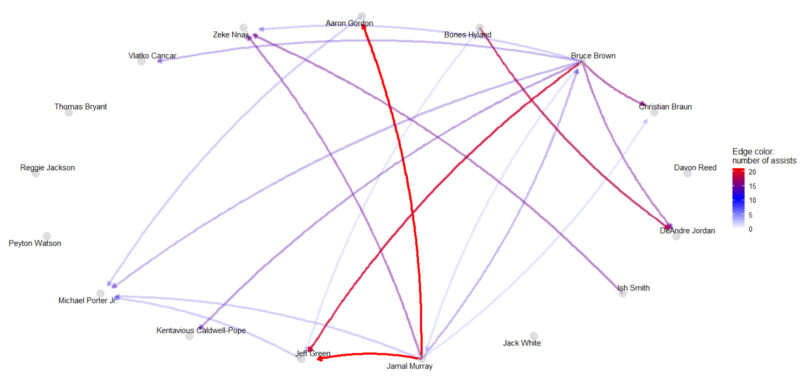
ヨキッチがコート上にいない場合、アシストの中心的プレイヤーはマレーに変わり、そのマレーからのアシストはゴードンとジェフ・グリーンに集中していることが読み取れます。
また、マレー以外でアシストを多く供給しているプレイヤーとしてはブルース・ブラウンが挙げられ、そのアシストに関してもジェフ・グリーンへのアシストが比較的多くなっていることが分かります。
ここではヨキッチの試合出場の有無により、チーム内のアシストネットワークがどのように変化するのかを確認していきました。
次は、1ショットあたりの平均得点と、1ショットを放つまでのplaylength※1の平均値に焦点をあてて、ヨキッチの試合出場の有無が与えるチームへの影響を見ていきたいと思います。
※1 playlengthとは、プレイヤーがシュートを放った場合に、そのシュートの直前のイベントからそのシュートを放つまでに何秒経過していたのかを表す項目です。例えば、リバウンドを獲得(直前のイベント)した後、その5秒経過後にシュートを放ったのであればplaylengthは「5」となります。また、対戦チームのターンオーバー(直前のイベント)の後、その10秒経過後にシュートを放ったのであればplaylengthは「10」となります。
なお、上記のグラフを出力するためのコマンドは下記のとおりです。
> library(BasketballAnalyzeR) #パッケージBasketballAnalyzeRの読み込み
> dts.PbP.2223 <- read.csv(file="PbP. BDB_2223.csv") # PbP. BDB2223の読み込み
> PbP2223 <- PbPmanipulation(dts.PbP.2223) # PbPmanipulation関数でPbP2223を作成
> PbP2223.DEN <- subset(PbP2223, team=="DEN") #PbP2223からteamがDENと一致するデータを抽出し、PbP2223.DENへ格納
> PbP2223.den <- PbP2223.DEN[!(PbP2223.DEN$event_type=="shot" & PbP2223.DEN$result=="missed"),]
#PbP2223.DENのevent_type欄がshotと一致し、かつresult欄がmissedに一致するデータを除外し、除外後のPbP2223.DENをPbP2223.denへ格納
> netdataden <- assistnet(PbP2223.den) #assistnet関数でアシスト数などを集計しnetdatadenへ格納
> plot(netdataden, layout="circle", edge.thr=20) #エッジ表示の閾値を20、ネットワークの形をサークルと指定し、netdatadenを用いてグラフを出力
> cols <- paste0(c("a","h"), rep(1:5, each=2)) #paste0関数でa1-a5, h1-h5の文字列を作成し、colsへ格納
> PbP2223.den.NJ0 <- PbP2223.den[!apply(PbP2223.den[,cols], 1, "%in%", x="Nikola Jokic"),]
#PbP2223.denのcolsに該当する列にNikola Jokicが含まれる場合はその行を!apply関数で除外し、除外後のPbP2223.denをPbP2223.den.NJ0へ格納
> netdataden.NJ0 <- assistnet(PbP2223.den.NJ0)
> plot(netdataden.NJ0, layout="circle", edge.thr=10)ヨキッチの試合出場の有無が与えるチームへの影響
1ショットあたりの平均得点、1ショットを放つまでのplaylengthの平均値の算出<ヨキッチの存在がオフェンス面で好循環を生む>
1ショットあたりの平均得点の算出過程と、1ショットを放つまでのplaylengthの平均値の算出過程は、下記のとおりです。
> PbP2223.DEN.NJ0 <- PbP2223.DEN[!apply(PbP2223.DEN[,cols], 1, "%in%", x="Nikola Jokic"),]
# PbP2223.DENのcolsに該当する列にNikola Jokicが含まれる場合はその行を!apply関数で除外し、除外後のPbP2223.DEN をPbP2223.DEN.NJ0へ格納
> PbP2223.DEN.NJ0 <- subset(PbP2223.DEN.NJ0, ShotType=="2P" | ShotType=="3P")
# PbP2223.DEN.NJ0からShotTypeが2Pと3Pに一致するデータを抽出し、PbP2223.DEN.NJ0へ格納
> pNJ0 <- mean(PbP2223.DEN.NJ0$points) #mean関数でPbP2223.DEN.NJ0のpoints欄の平均値を算出し、pNJ0へ格納
> plNJ0 <- mean(PbP2223.DEN.NJ0$playlength) #mean関数でPbP2223.DEN.NJ0のplaylength欄の平均値を算出し、plNJ0へ格納
> PbP2223.DEN.NJ1 <- PbP2223.DEN[apply(PbP2223.DEN[,cols], 1, "%in%", x="Nikola Jokic"),]
# PbP2223.DENのcolsに該当する列にNikola Jokicが含まれる場合はその行をapply関数で抽出し、抽出後のPbP2223.DEN をPbP2223.DEN.NJ1へ格納
> PbP2223.DEN.NJ1 <- subset(PbP2223.DEN.NJ1, ShotType=="2P" | ShotType=="3P")
> pNJ1 <- mean(PbP2223.DEN.NJ1$points)
> plNJ1 <- mean(PbP2223.DEN.NJ1$playlength)
また、実際の各数値は下記のとおりです。
> pNJ0 #ヨキッチ出場なしの1ショットあたりの平均得点
[1] 1.039693
> plNJ0 #ヨキッチ出場なしの1ショットを放つまでのplaylengthの平均値
[1] 12.52625
> pNJ1 #ヨキッチ出場ありの1ショットあたりの平均得点
[1] 1.193736
> plNJ1 #ヨキッチ出場ありの1ショットを放つまでのplaylengthの平均値
[1] 11.69699上記の計算結果を確認すると、ヨキッチがコート上にいないときの1ショットあたりの平均得点は約1.04点であるのに対して、ヨキッチがコート上にいるときの同平均得点は約1.19点となっており、約0.15点だけ高いことが分かります。
また、ヨキッチがコート上にいないときの1ショットを放つまでのplaylengthの平均値は約12.53秒であるのに対して、ヨキッチがコート上にいるときの同平均値は約11.70秒となっており、約0.83秒だけ早いことが分かります。
以上のことから、ヨキッチが試合に出場することで、1ショットあたりに見込まれる獲得点数が増加しオフェンスの効率が良くなり、さらには1ショットを放つまでのサイクルが早くなることで、オフェンス面で好循環が生まれると考えられます。
※なお、今回算出した2つの平均値の間で見られた差異が、統計的に有意な差と認められるかどうかは、以降に続くこれらの平均値に対する統計的仮説検定をご参考ください。
【参考】2標本の平均に関する検定
独立な2群のt検定
前述した2つの平均値に関して、2標本の平均に関する検定を統計ソフトRで行っていきます。
帰無仮説H0を「μ1=μ2(2つの母平均は等しい)」、対立仮説H1を「μ1≠μ2(2つの母平均は等しくない)」と設定し、以下の算式で算出される検定統計量tに関して、有意水準5%で両側検定を行います。(※等分散性の検定に関しては、後述箇所をご参考ください。)
$$t=\dfrac{\overline{X}_{1}-\overline{X}_{2}}{\sqrt{\dfrac{\left( n_{1}-1\right) s_{1}^{2}+\left( n_{2}-1\right) s_{2}^{2}}{n_{1}+n_{2}-2}\left( \dfrac{1}{n_{1}}+\dfrac{1}{n_{2}}\right) }}$$
\(\overline{X}_{1}\)は1群目の標本平均、\(n_{1}\)は1群目のサンプルサイズ、\(s_{1}^{2}\)は1群目の不偏分散、\(\overline{X}_{2}\)は2群目の標本平均、\(n_{2}\)は2群目のサンプルサイズ、\(s_{2}^{2}\)は2群目の不偏分散を表します。
なお、結果のみを簡単に示していきますが、結果の解釈などについては、統計WEBサイト「24-4. 対応のない2標本t検定」や記事の最後に掲載している参考書籍を参照しています。
1ショットあたりの平均得点に関するt検定は、下記のとおりです。
> t.test(PbP2223.DEN.NJ0$points, PbP2223.DEN.NJ1$points, var.equal=TRUE)
Two Sample t-test
data: PbP2223.DEN.NJ0$points and PbP2223.DEN.NJ1$points
t = -5.8827, df = 8805, p-value = 0.000000004183
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
-0.2053731 -0.1027129
sample estimates:
mean of x mean of y
1.039693 1.193736
p値(p-value)が0.000000004183となっており、有意水準の5%(0.05)よりも小さくなっているため、有意差が認められます。
そのため、帰無仮説H0「μ1=μ2(2つの母平均は等しい)」が棄却され、対立仮説H1「μ1≠μ2(2つの母平均は等しくない)」が採択されることになります。
続いて、1ショットを放つまでのplaylengthの平均値に関するt検定は、下記のとおりです。
> t.test(PbP2223.DEN.NJ0$playlength, PbP2223.DEN.NJ1$playlength, var.equal=TRUE)
Two Sample t-test
data: PbP2223.DEN.NJ0$playlength and PbP2223.DEN.NJ1$playlength
t = 5.3618, df = 8805, p-value = 0.00000008449
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
0.5260862 1.1324286
sample estimates:
mean of x mean of y
12.52625 11.69699
p値(p-value)が0.00000008449となっており、有意水準の5%(0.05)よりも小さくなっているため、有意差が認められます。
そのため、こちらも帰無仮説H0「μ1=μ2(2つの母平均は等しい)」が棄却され、対立仮説H1「μ1≠μ2(2つの母平均は等しくない)」が採択されることになります。
等分散性の検定
上記のt検定を実施するための前提条件として、分散の等質性を満たす必要があります。
ここでは、前述した2つの変数(1ショットごとの得点、1ショットを放つまでのplaylengthの長さ)に関して、等分散性の検定を統計ソフトRで行っていきます。
帰無仮説H0を「\(\sigma _{1}^{2}\)=\(\sigma _{2}^{2}\)(2つの母分散は等しい)」、対立仮説H1を「\(\sigma _{1}^{2}\)≠\(\sigma _{2}^{2}\)(2つの母分散は等しくない)」と設定し、以下の算式で算出される検定統計量Fに関して、有意水準5%で両側検定を行います。
$$F=\dfrac{s_{1}^{2}}{s_{2}^{2}}$$
なお、結果のみを簡単に示していきますが、結果の解釈などについては、統計WEBサイト「28-4. 等分散性の検定」や記事の最後に掲載している参考書籍を参照しています。
1ショットごとの得点に関する分散の等質性の検定は、下記のとおりです。
> var.test(PbP2223.DEN.NJ0$points, PbP2223.DEN.NJ1$points)
F test to compare two variances
data: PbP2223.DEN.NJ0$points and PbP2223.DEN.NJ1$points
F = 1.0138, num df = 3123, denom df = 5682, p-value = 0.6608
alternative hypothesis: true ratio of variances is not equal to 1
95 percent confidence interval:
0.953368 1.078694
sample estimates:
ratio of variances
1.013812
p値(p-value)が0.6608となっており、有意水準の5%(0.05)よりも大きくなっているため、分散比1.013812に有意な差は認められないことになります。
そのため、帰無仮説H0「\(\sigma _{1}^{2}\)=\(\sigma _{2}^{2}\)(2つの母分散は等しい)」は棄却されず、分散の等質性の仮定が満たされることになります。
続いて、1ショットを放つまでのplaylengthに関する分散の等質性の検定は、下記のとおりです。
> var.test(PbP2223.DEN.NJ0$playlength, PbP2223.DEN.NJ1$playlength)
F test to compare two variances
data: PbP2223.DEN.NJ0$playlength and PbP2223.DEN.NJ1$playlength
F = 1.0187, num df = 3123, denom df = 5682, p-value = 0.5531
alternative hypothesis: true ratio of variances is not equal to 1
95 percent confidence interval:
0.9580104 1.0839469
sample estimates:
ratio of variances
1.018749
p値(p-value)が0.5531となっており、有意水準の5%(0.05)よりも大きくなっているため、分散比1.018749に有意な差は認められないことになります。
そのため、こちらも帰無仮説H0「\(\sigma _{1}^{2}\)=\(\sigma _{2}^{2}\)(2つの母分散は等しい)」は棄却されず、分散の等質性の仮定が満たされることになります。
次回について
今回はネットワーク分析を用いて、2022-23シーズンにおけるナゲッツのアシストネットワークを確認していきました。
また、1ショットあたりの平均得点と、1ショットを放つまでのplaylengthの平均値に焦点をあて、アシストの中心的プレイヤーであるヨキッチが持つチームへの影響力もあわせて確認しました。
次回記事も引き続きナゲッツに注目し、アシストに付随する各スタッツの分析を行いたいと思います。
なお、本記事は、記事の最後に紹介している書籍を参考にして作成しています。
それでは、今回のトラッシュトークは以上です。
【参考書籍】
Paola Zuccolotto and Marica Manisera (2020), Basketball Data Science – with Applications in R. Chapman and Hall/CRC. ISBN 9781138600799.
※本書籍の紹介記事を書いていますので、よろしければご参考ください。
山田剛史、杉澤武俊、村井潤一郎(2008)『Rによるやさしい統計学』オーム社.
東京大学教養学部統計学教室編(1991)『統計学入門(基礎統計学Ⅰ)』東京大学出版会.