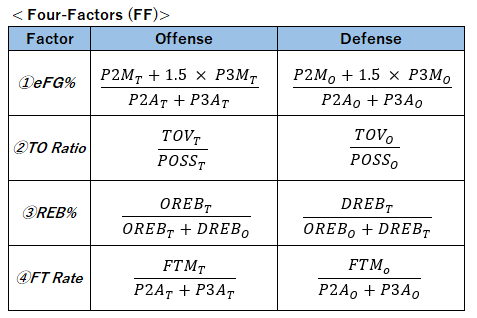
今回は、前回の記事で算出した各スタッツを用いて、統計ソフトRによる散布図の作成方法を紹介していきたいと思います。
各スタッツにおけるチームの分布とプレーオフ進出の有無に関連性があるかどうかを確認するために、散布図を作成する際には、チームのプレーオフ進出の有無を色分けで区別していきます。
なお、前回の記事で紹介したPOSSに関しては、仮に試合の延長戦(オーバータイム)があった場合はその数値が必然的に増えてしまいます。
延長戦を戦った時間は各チームによってばらつきがあることから、POSSの数値を各チームで単純に比較することは適切ではない可能性があります。
上記の理由により、今回はPOSSの散布図の作成を省略しています。
まずは、プレーオフ進出の情報を前回の記事で作成したデータセットfourfactors2223に追加するところから始めたいと思います。
※データ分析を実践する際に参考にしている書籍『Basketball Data Science: With Applications in R』の紹介記事も書きましたので、よろしければご確認ください。
NBAプレーオフ進出情報をデータセットfour factorsへ追加
はじめに、Tadd2223(過去記事参照)で集計されているプレーオフ進出の情報を下記のようにPlayoffへ格納します。
> Playoff <- Tadd2223$Playoff
> Playoff
[1] "Y" "Y" "Y" "N" "N" "Y" "N" "Y" "N" "Y" "N" "N" "Y" "Y" "Y" "Y" "Y" "Y" "N" "Y" "N" "N" "Y" "Y" "N" "Y" "N" "N" "N" "N"次に、data. frame 関数によりfourfactors2223とPlayoffを用いてデータフレームfourfactors2223POを作成します。
> fourfactors2223PO <- data.frame(fourfactors2223, Playoff)データフレームfourfactors2223POの出力は下記のとおりです。
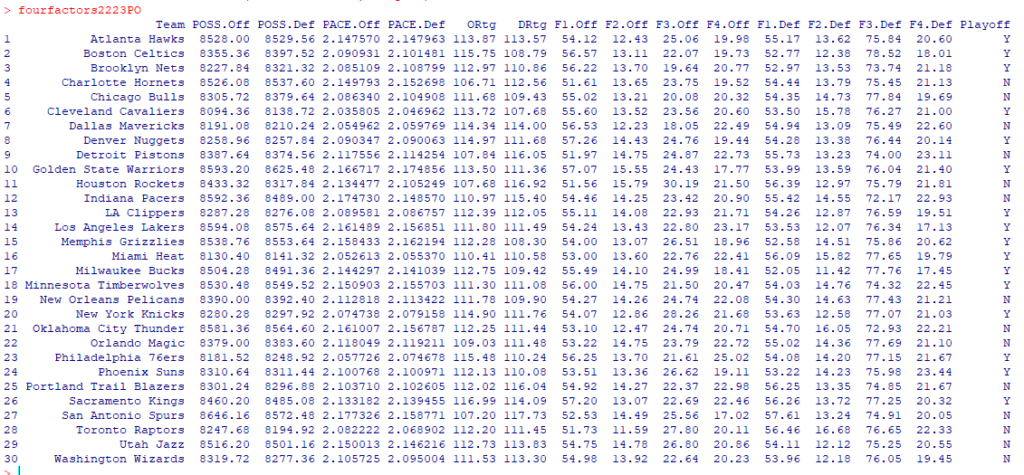
右端の項目にPlayoffの情報が追加されていることがわかります。
今回は上記のデータフレームfourfactors2223POをベースに、各スタッツの散布図の作成を進めていきたいと思います。
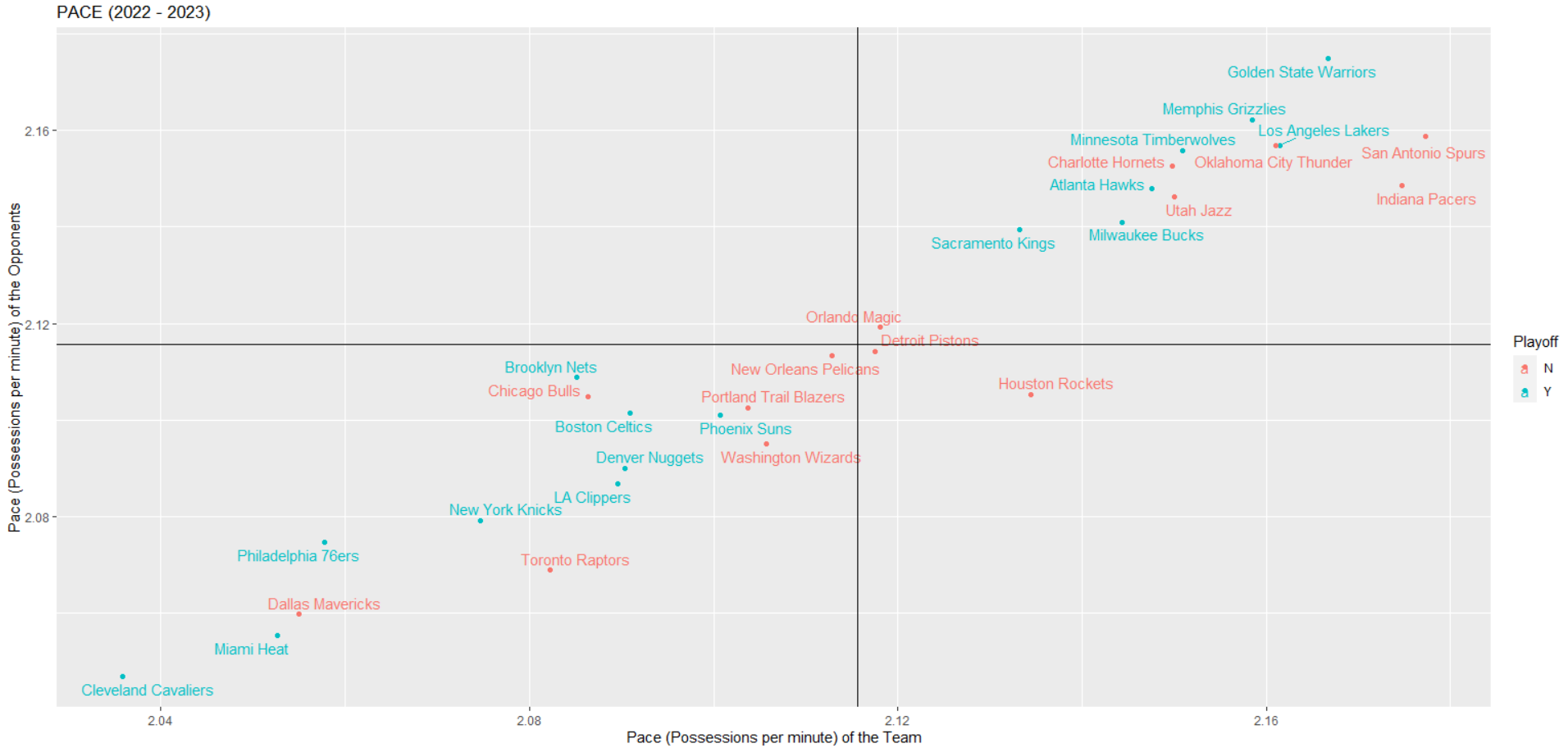
PACEの散布図<攻守に時間をかけるのはクリーブランド・キャバリアーズ>
まずはPACEの散布図から作成していきます。
プロットを出力するために下記のようにコマンドを入力します。
> ggplot(data=fourfactors2223PO, aes(x=PACE.Off, y=PACE.Def, color = Playoff, label=Team)) +
+ geom_point() +
+ ggrepel::geom_text_repel(aes(label = Team))+
+ geom_vline(xintercept =mean(fourfactors2223PO$PACE.Off))+
+ geom_hline(yintercept =mean(fourfactors2223PO$PACE.Def))+
+ labs(title = "PACE (2022 - 2023)")+
+ labs(x = "Pace (Possessions per minute) of the Team") +
+ labs(y = "Pace (Possessions per minute) of the Opponents")なお、下記2行のコマンドは、PACE.OffとPACE.Defの平均値を直線で示すために入力しています。(以降の各スタッツに関しても同様に処理します。)
geom_vline(xintercept =mean(fourfactors2223PO$PACE.Off))
geom_hline(yintercept =mean(fourfactors2223PO$PACE.Def))出力の結果は下記のようになります。
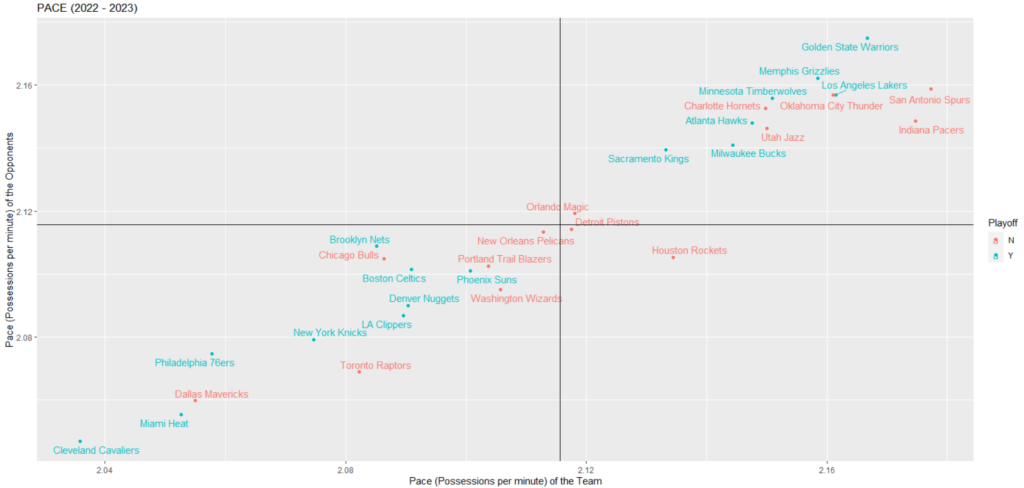
プレーオフ進出の有無がチームごとに色分けされており、水色がPlayoff進出あり、赤色が進出なしとなります。
左下のエリア周辺に位置するチームは相対的に試合テンポがゆっくりしていて、右上のエリア周辺に位置するチームは相対的に試合テンポが早いと考えられます。
クリーブランド・キャバリアーズが最も試合のテンポが遅く、次にマイアミ・ヒート、ダラス・マーベリックスが続きます。
試合テンポが早いチームに関しては、単独でこのチームが最も早いとは特定出来ないのですが、ゴールデンステイト・ウォリアーズ、メンフィス・グリズリーズ、オクラホマシティ・サンダー、ロサンゼルス・レイカーズ、サンアントニオ・スパーズ、インディアナ・ペイサーズの6チームが相対的に試合テンポの早いチームであると考えられます。
なお、プレーオフに進出したチームが一部のエリアに偏っているわけではないので、試合テンポの遅さ・早さとプレーオフ進出に関連性は無さそうです。
試合展開が遅いか、速いかはあくまでもそのチームの特性であり、その試合展開の違いにより試合を有利に運べたり、不利に追い込まれたりはしないと考えられます。
ORtg、DRtgの散布図<サクラメント・キングスに注目>
次に、ORtgとDRtgの散布図を作成します。
プロットを出力するために下記のようにコマンドを入力します。
> ggplot(data=fourfactors2223PO, aes(x=ORtg, y=DRtg, color = Playoff, label=Team)) +
+ geom_point() +
+ ggrepel::geom_text_repel(aes(label = Team))+
+ geom_vline(xintercept =mean(fourfactors2223PO$ORtg))+
+ geom_hline(yintercept =mean(fourfactors2223PO$DRtg))+
+ labs(title = "ORtg and DRtg (2022 - 2023)")+
+ labs(x = "Offensive Rating of the Team (ORtg)") +
+ labs(y = "Offensive Rating of the Opponents (DRtg)")出力の結果は下記のようになります。
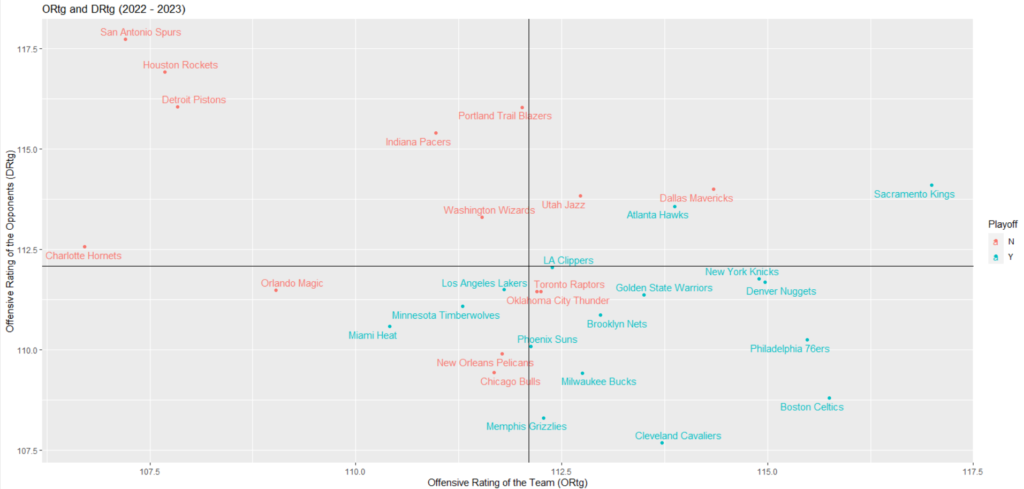
各エリアの特徴は下記の通りです。
- 右下のエリア : オフェンス効率性、ディフェンス効率性がともに高い
- 右上のエリア : オフェンス効率性は高いが、ディフェンス効率性が低い
- 左下のエリア : ディフェンス効率性は高いが、オフェンス効率性が低い
- 左上のエリア : オフェンス効率性、ディフェンス効率性がともに低い
プレーオフへ進出したチームの配置が右下のエリア周辺に偏っていることがわかります。
トロント・ラプターズとオクラホマシティ・サンダーについては、右下のエリアに入ってはいますが、惜しくもプレーイントーナメントで敗退となったチームです。
一方、アトランタ・ホークス、ロサンゼルス・レイカーズ、ミネソタ・ティンバーウルブズ、マイアミ・ヒートは右下のエリアに入っていませんが、プレーイントーナメントを勝ち上がることでプレーオフへの進出を決めています。
上記の散布図で気になる点は、右上のエリアに位置するサクラメント・キングスでしょうか。
サクラメント・キングス は、DRtgが平均値よりも大きいため相対的にディフェンス効率が悪いと判断できます。(ダラス・マーベリックスやユタ・ジャズと同水準のDRtg)
ですが、ORtgが全30チームの中で最も高く、後述するeFG% (Offence)、TO Ratio (Offence)、FT Rate (Offence)は平均値よりも優れた値をとっています。
そのため、サクラメント・キングスに関しては、ディフェンス効率が良いとは言えないが、それを補うオフェンスの能力の高さがあり、レギュラーシーズンを通してその能力を発揮できたものと考えられます。
eFG%の散布図<マイアミ・ヒートに注目>
次に、eFG%の散布図を作成します。
プロットを出力するために下記のようにコマンドを入力します。
> ggplot(data=fourfactors2223PO, aes(x=F1.Off, y=F1.Def, color = Playoff, label=Team)) +
+ geom_point() +
+ ggrepel::geom_text_repel(aes(label = Team))+
+ geom_vline(xintercept =mean(fourfactors2223PO$F1.Off))+
+ geom_hline(yintercept =mean(fourfactors2223PO$F1.Def))+
+ labs(title = "Factor 1:eFG% (2022 - 2023)")+
+ labs(x = "eFG% (Offense)") +
+ labs(y = "eFG% (Defense)")出力の結果は下記のようになります。
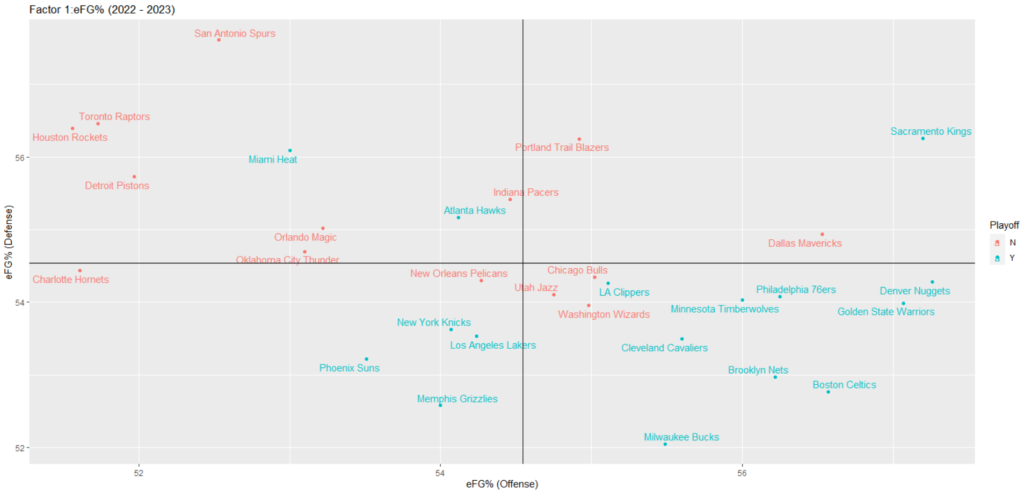
おおまかな傾向ではありますが、こちらもプレーオフへ進出したチームの配置が右下のエリア周辺に偏っているように見えます。
前述したとおりサクラメント・キングスのオフェンス能力もさることながら、上記の散布図で注目すべき点は、マイアミ・ヒートの位置だと思います。
マイアミ・ヒートは、決して良いとは言えないレギュラーシーズンの状態からプレーオフの第8シードを勝ち取り、NBAファイナルまで駒を進めました。(第8シードからのファイナル進出は1999年のニューヨーク・ニックス以来の出来事。)
上記の散布図を眺めていると、改めてそのすごさを実感することができます。
マイアミ・ヒートに関しては、前述のとおり試合のテンポが相対的に遅く(PACEの散布図参照)、ディフェンス効率性が相対的に高い(DRtgの散布図参照)チームとなっています。
また、後述するTO Ratio(Defense)とREB% (Defense)は、平均値よりも優れた値をとっています。
これらのことから、マイアミ・ヒート は常に自チームの試合ペースを乱すことなく、堅実なディフェンスを続けることで不利な状況をはねのけ、最終的にNBAファイナルへ進むことができたとも考えられます。
TO Ratioの散布図
次に、TO Ratioの散布図を作成します。
プロットを出力するために下記のようにコマンドを入力します。
> ggplot(data=fourfactors2223PO, aes(x=F2.Off, y=F2.Def, color = Playoff, label=Team)) +
+ geom_point() +
+ ggrepel::geom_text_repel(aes(label = Team))+
+ geom_vline(xintercept =mean(fourfactors2223PO$F2.Off))+
+ geom_hline(yintercept =mean(fourfactors2223PO$F2.Def))+
+ labs(title = "Factor 2:TO Ratio (2022 -2023)")+
+ labs(x = "TO Ratio (Offense)") +
+ labs(y = "TO Ratio (Defense)")出力の結果は下記のようになります。
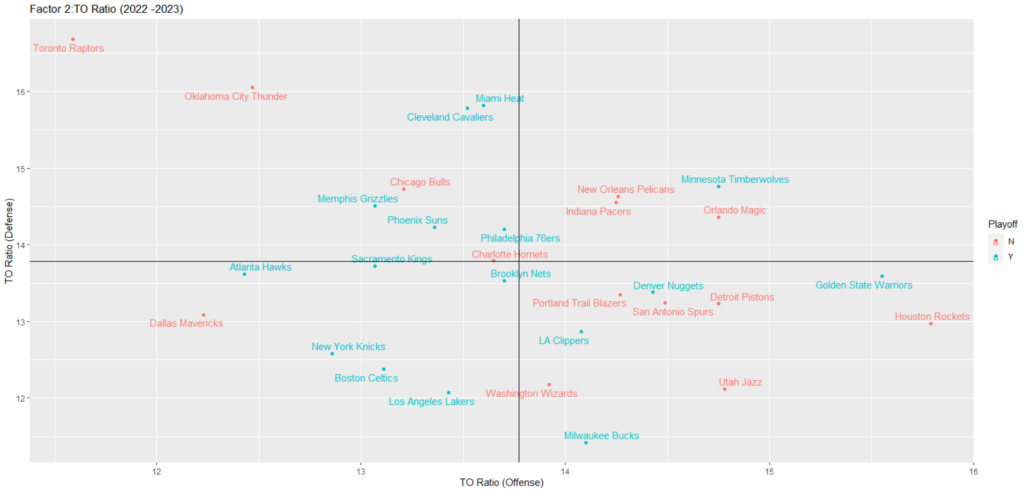
上記の散布図に関しては、例えば、チームのターンオーバーが相対的に少なく、対戦チームのターンオーバーが相対的に多ければ左上のエリアに位置することになります。
散布図を見る限り、プレーオフに進出したチームが一部のエリアに偏っているわけではないので、TO Ratioとプレーオフ進出に関連性は無さそうに見えます。
REB%の散布図
次に、REB%の散布図を作成します。
プロットを出力するために下記のようにコマンドを入力します。
> ggplot(data=fourfactors2223PO, aes(x=F3.Off, y=F3.Def, color = Playoff, label=Team)) +
+ geom_point() +
+ ggrepel::geom_text_repel(aes(label = Team))+
+ geom_vline(xintercept =mean(fourfactors2223PO$F3.Off))+
+ geom_hline(yintercept =mean(fourfactors2223PO$F3.Def))+
+ labs(title = "Factor 3:REB% (2022 - 2023)")+
+ labs(x = "REB% (Offense)") +
+ labs(y = "REB% (Defense)")
出力の結果は下記のようになります。
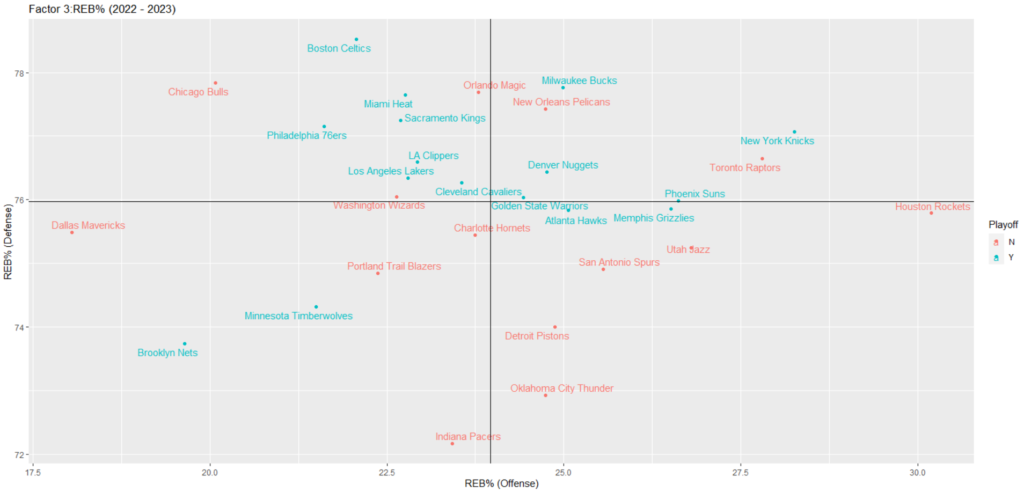
REB% (Defense)に関しては、ミネソタ・ティンバーウルブズとブルックリン・ネッツの例外はありますが、平均値付近かそれ以上のエリアにプレーオフ進出チームが位置している傾向が読み取れます。
上記の散布図を眺めていると、オフェンスリバウンドの強さとチームの強さに関連性は無いのだろうかという疑問が浮かんできました。
オフェンスリバウンドを獲得するということは、シュートを外すことが前提にあるので、REB% (Offense)の高い数値が優れたスタッツであるとは一概には言えないとも考えられます。
そこで、eFG% (Offense)とREB% (Offense)の散布図も作成してみます。
プロットを出力するために下記のようにコマンドを入力します。
> ggplot(data=fourfactors2223PO, aes(x=F1.Off, y=F3.Off, color = Playoff, label=Team)) +
+ geom_point() +
+ ggrepel::geom_text_repel(aes(label = Team))+
+ geom_vline(xintercept =mean(fourfactors2223PO$F1.Off))+
+ geom_hline(yintercept =mean(fourfactors2223PO$F3.Off))+
+ labs(title = "eFG% and REB% (2022 - 2023)")+
+ labs(x = "eFG% (Offense)") +
+ labs(y = "REB% (Offense)")出力の結果は下記のようになります。
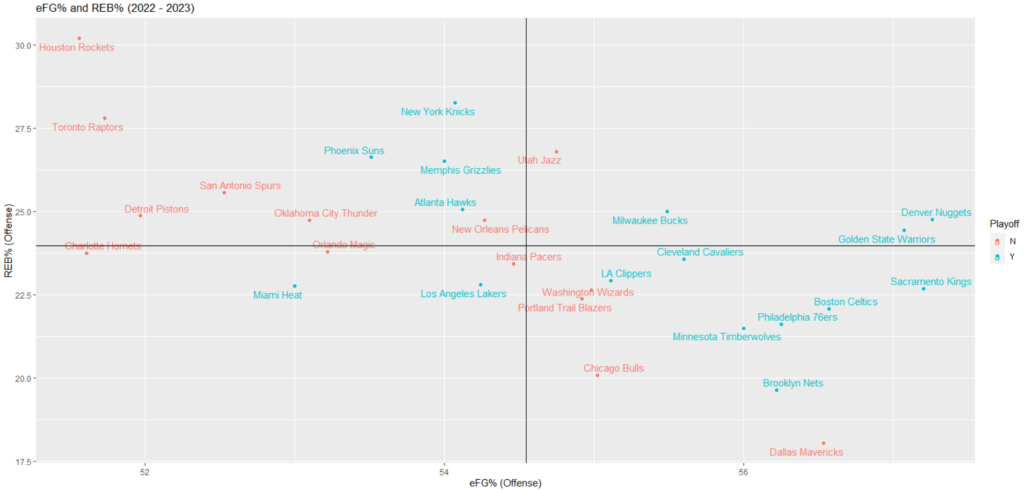
おおまかな傾向として、左上のエリア(eFG% (Offense)が相対的に低く、REB% (Offense)が相対的に高い)周辺と右下のエリア(eFG% (Offense)が相対的に高く、REB% (Offense)が相対的に低い)周辺に各チームが散らばっていることが見て取れます。
データの散らばり方から負の相関がありそうなため、相関係数を下記の通り算出してみます。
> cor(fourfactors2223PO$F1.Off, fourfactors2223PO$F3.Off)
[1] -0.5678753相関係数が-0.5678753となったため、eFG% (Offense) とREB% (Offense)の間には中程度の負の相関関係があると言えそうです。※1
このことから、オフェンスリバウンドの強さの裏には、eFG%の低さという欠点が隠れている可能性が示唆されます。
※1 相関関係の強弱の判断に関しては、山田剛史、杉澤武俊、村井潤一郎(2008)『Rによるやさしい統計学』オーム社のp 62 – p64を参考にしています。
FT Rateの散布図
最後に、FT Rateの散布図を作成します。
プロットを出力するために下記のようにコマンドを入力します。
> ggplot(data=fourfactors2223PO, aes(x=F4.Off, y=F4.Def, color = Playoff, label=Team)) +
+ geom_point() +
+ ggrepel::geom_text_repel(aes(label = Team))+
+ geom_vline(xintercept =mean(fourfactors2223PO$F4.Off))+
+ geom_hline(yintercept =mean(fourfactors2223PO$F4.Def))+
+ labs(title = "Factor 4:FT Rate (2022 - 2023)")+
+ labs(x = "FT Rate (Offense)") +
+ labs(y = "FT Rate (Defense)")出力の結果は下記のようになります。
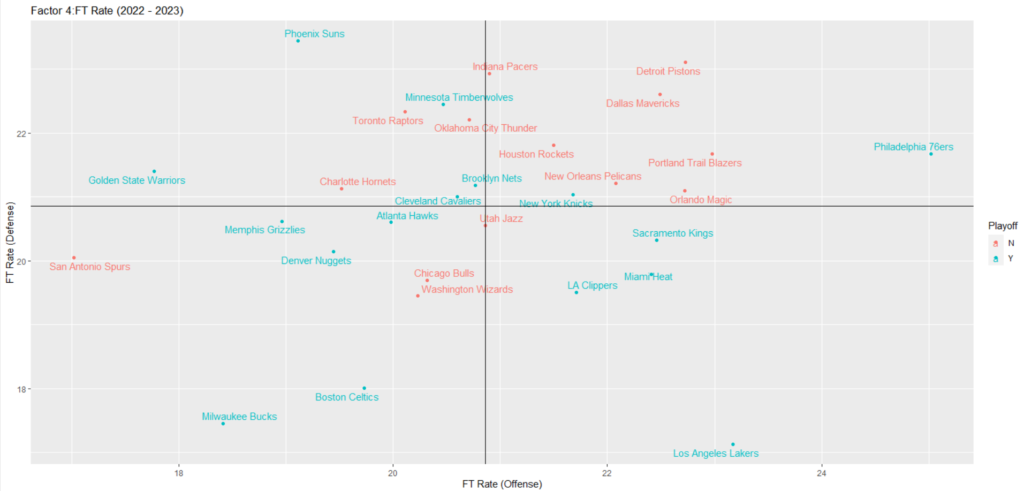
こちらもTO Ratioと同様に、プレーオフに進出したチームが一部のエリアに偏っているわけではないので、FT Rateとプレーオフ進出に関連性は無さそうです。
おわりに
以上、今回は前回の記事で算出した各スタッツの散布図を作成していきました。
散布図を見る限りORtgとDRtg、eFG%、REB%に関しては、プレーオフ進出の有無によりデータの散らばり方に一定の傾向が見られました。
散布図の作成はデータ分析の基本だと思いますので、今後も気になるデータに関しては散布図でデータの分布を確認していきたいと思います。
なお、本記事は、記事の最後に紹介している書籍を参考にして作成しています。
それでは、今回のトラッシュトークは以上です。
【参考書籍】
Paola Zuccolotto and Marica Manisera (2020), Basketball Data Science – with Applications in R. Chapman and Hall/CRC. ISBN 9781138600799.
※本書籍の紹介記事を書いていますので、よろしければご参考ください。
山田剛史、杉澤武俊、村井潤一郎(2008)『Rによるやさしい統計学』オーム社.