今回は、アシスト関連のスタッツを使って、統計ソフトRによる散布図の作成方法を紹介していきます。
散布図を作成する際には、獲得点数の多寡に応じて、プロットされるプレイヤーの色分けも行いたいと思います。
データは2022–23レギュラーシーズンのPbox(過去記事参照)を使用します。
まずは、アシスト数とターンオーバー数の散布図からみていきます。
※データ分析を実践する際に参考にしている書籍『Basketball Data Science: With Applications in R』の紹介記事も書きましたので、よろしければご確認ください。
ASTとTOVの散布図<ジェームズ・ハーデンの位置を確認>
アシスト数(AST)とターンオーバー数(TOV)の散布図は下記のとおりです。
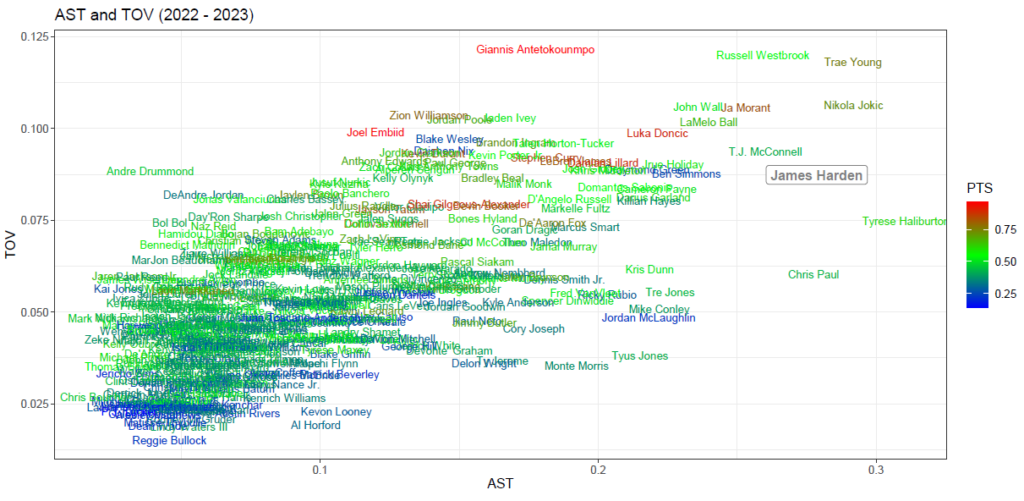
横軸はアシスト数(AST)を、縦軸はターンオーバー数(TOV)を表しています。
獲得点数(PTS)については、その多さによって色分けをしており、獲得点数が少なければ青色、平均的であれば緑色、多ければ赤色で表示されます。
また、アシスト数(AST)、ターンオーバー数(TOV)、獲得点数(PTS)はすべて1MIN(分)あたりの数値に変換しており、プロットするプレイヤーについては出場時間500MIN以上のプレイヤーを抽出しています。
上記の散布図について、左下のエリアはプレイヤーが多数いて判別が不可能であるが、右上あたりのエリアに注目すると、それぞれのプレイヤーに関して下記の傾向を読み取ることができます。
- アシスト数の多さに対して相対的にターンオーバーが少ない:ジェームズ・ハーデンはこの傾向を持っている(※散布図上では四角枠で強調しています)。その他のプレイヤーだとタイリース・ハリバートン、クリス・ポールが該当する。
- アシスト数に対して相対的にターンオーバーが多い:ヤニス・アデトクンボが該当する(※1MINあたりの獲得点数は高い)。
- アシスト数もターンオーバー数もどちらも多い:ラッセル・ウェストブルック、トレイ・ヤング、ニコラ・ヨキッチが該当する。
なお、今回は1試合あたりのアシスト数ではなく、1MINあたりのアシスト数で比較しているため、ジェームズ・ハーデンではなくタイリース・ハリバートンのアシスト数が最も多くなっています。
上記の散布図を眺めると、全体的にアシスト数が多いプレイヤーは、その増加に応じてターンオーバー数も増加していくという傾向を読み取ることができます。
データの散らばり方に右上がりの傾向が見られるため、正の相関関係が想定されます。
そこで、相関係数を算出すると下記のとおり0.6447521となるため、中程度の正の相関関係があることがわかります。※1
> cor(X$AST, X$TOV)
[1] 0.6447521※1 相関関係の強弱の判断に関しては、山田剛史、杉澤武俊、村井潤一郎(2008)『Rによるやさしい統計学』オーム社のp 62 – p64を参考にしています。
アシストをするためにボールをコントロールする機会が多くなれば、その分だけターンオーバーの場面が増えるというのは当然のことではあります。
ですが、その中でもジェームズ・ハーデンは、オフェンス時にはターンオーバーが発生しないよう丁寧にボールをコントロールしながら、高水準でチームへアシストを供給していたことが想定されます。
なお、散布図を出力するためのコマンドは下記のとおりです。
> Pbox2223M <- subset(Pbox2223, MIN>=500) #MIN500以上のプレイヤーを抽出
> attach(Pbox2223M) #attach関数でTbox2223を指定
> X <- data.frame(AST, TOV, PTS)/MIN #各スタッツのMINあたりの数値をdata.frame関数でまとめてXに格納
> detach(Pbox2223M) #detach関数でTbox2223を指定から外す
> mypal <- colorRampPalette(c("blue","green","red")) # colorRampPalette関数でPTSの色分けをするためのカラーパレットを作成
> JH <- which(Pbox2223M$Player=="James Harden") #which関数でPlayer欄から"James Harden"と一致する項目を指定し、JHへ格納
> scatterplot(X, data.var=c("AST","TOV"), z.var="PTS", labels=Pbox2223M$Player, palette=mypal, subset=JH, title="AST and TOV (2022 - 2023)")
#散布図を作成するためのコマンド。z.var="PTS"で3つめの変数を指定、palette=mypalで色分けを指定、subset=JHでJames Hardenを強調する。前回の記事では、アシスト数が多いプレイヤーは2Pシュート成功数、フリースロー成功数、スティール数のほうも比較的良さそうな傾向があることを指摘しました。
そこで、次はアシスト数と2Pシュート成功数、フリースロー成功数、スティール数の散布図を作成したいと思います。
ASTと3つのスタッツの関係を確認
2Pシュート成功数(P2M)から順番に、フリースロー成功数(FTM)、スティール数(STL)との散布図を作成していきます。
ASTとP2Mの散布図<ニコラ・ヨキッチが好スタッツ>
まずは、アシスト数と2Pシュート成功数(P2M)の散布図を示します。
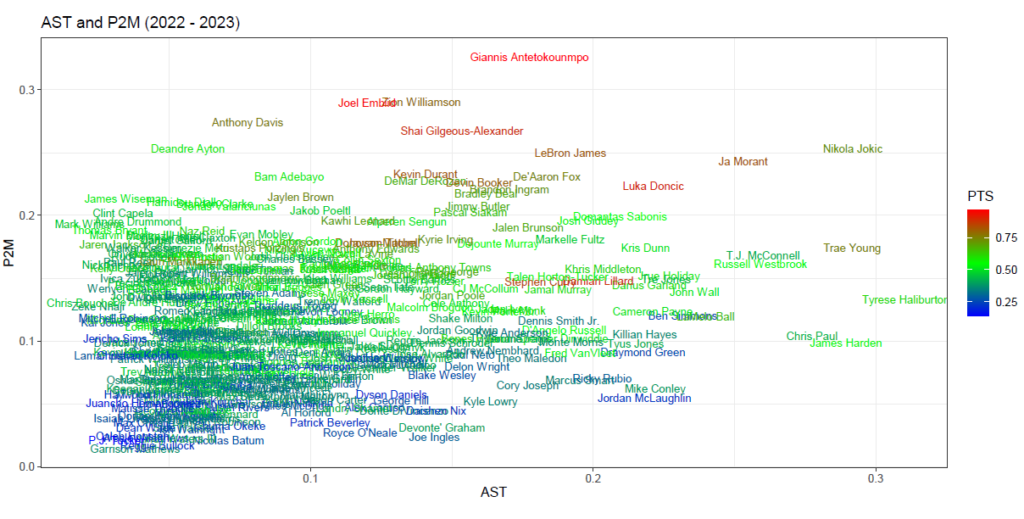
散布図を確認すると、アシスト数と2Pシュート成功数がともに多いのは、ニコラ・ヨキッチであることがわかります。
データの散らばり方から判断するに、強い正の相関関係は見られそうにありません。
相関係数を算出すると下記のとおり、0.2332765となり、相関関係の程度は弱いと判断できます。※1
> cor(Y$AST, Y$P2M)
[1] 0.2332765なお、散布図を出力するためのコマンドは下記のとおりです。
> attach(Pbox2223M)
> Y <- data.frame(AST, P2M, FTM, STL, PTS)/MIN
> detach(Pbox2223M)
> scatterplot(Y, data.var=c("AST","P2M"), z.var="PTS", labels=Pbox2223M$Player, palette=mypal, title="AST and P2M (2022 - 2023)")ASTとFTMの散布図<トレイ・ヤングが好スタッツ>
次に、アシスト数とフリースロー成功数(FTM)の散布図を示します。
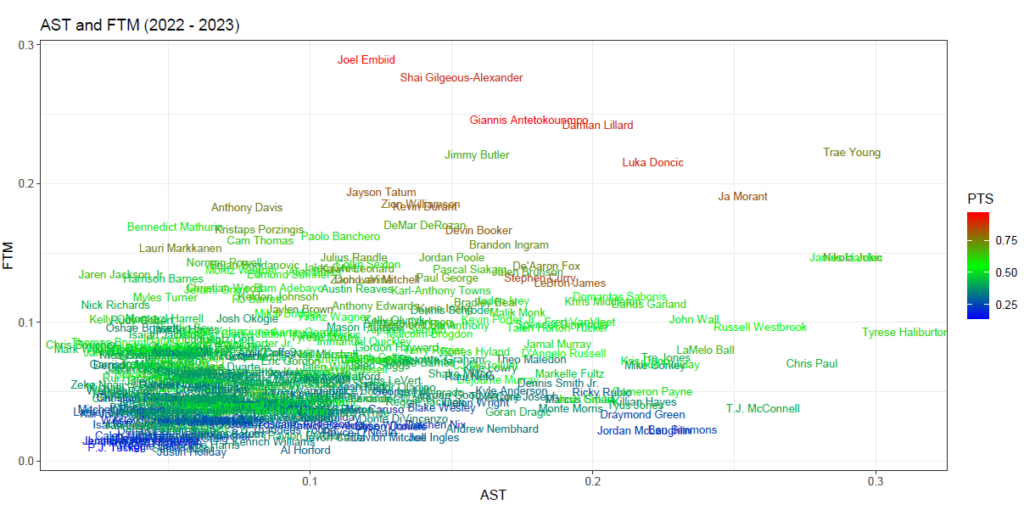
散布図を確認すると、アシスト数とフリースロー成功数がともに多いのは、トレイ・ヤングであることがわかります。
データの散らばり方から判断するに、こちらも2Pシュート成功数と同様に、強い正の相関関係は見られそうにありません。
相関係数を算出すると下記のとおり、0.3296864となり、相関関係の程度は弱いと判断できます。※1
> cor(Y$AST, Y$FTM)
[1] 0.3296864なお、散布図を出力するためのコマンドは下記のとおりです。
> scatterplot(Y, data.var=c("AST","FTM"), z.var="PTS", labels=Pbox2223M$Player, palette=mypal, title="AST and FTM (2022 - 2023)")ASTとSTLの散布図<タイリース・ハリバートンが好スタッツ>
最後に、アシスト数とスティール数(STL)の散布図を示します。
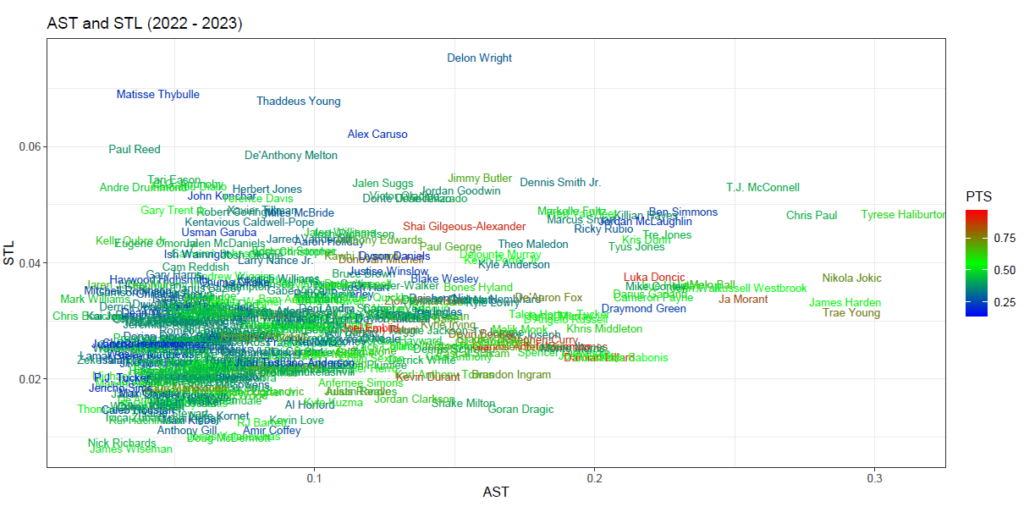
散布図を確認すると、アシスト数とスティール数がともに多いのは、タイリース・ハリバートンであることがわかります。
データの散らばり方から判断するに、こちらも2Pシュート成功数とフリースロー成功数と同様に、強い正の相関関係は見られそうにありません。
相関係数を算出すると下記のとおり、0.3153809となり、相関関係の程度は弱いと判断できます。※1
> cor(Y$AST, Y$STL)
[1] 0.3153809なお、散布図を出力するためのコマンドは下記のとおりです。
> scatterplot(Y, data.var=c("AST","STL"), z.var="PTS", labels=Pbox2223M$Player, palette=mypal, title="AST and STL (2022 - 2023)")前回の記事では、アシスト数と上記3つのスタッツの関係をレーダーチャートで見て直感的に判断しました。
今回は散布図を作成することによって、それらの相関関係の強弱が視覚的に分かりやすくなったと思います。
また、相関係数を算出すれば、その相関関係の強弱が数値化されますので、各スタッツ間の関係がさらに解釈しやすいものへとなりました。
おわりに
今回は、アシスト数とターンオーバー数の関係を散布図を使って確認し、さらに、2Pシュート成功数、フリースロー成功数、スティール数との散布図もあわせて確認しました。
アシスト数とターンオーバー数の間には中程度の正の相関関係が見られた一方で、2Pシュート成功数、フリースロー成功数、スティール数のほうは程度の弱い正の相関関係が見られました。
今回は、アシストのスタッツを取り上げることもあって、2022-23シーズンのアシスト王のジェームズ・ハーデンにも注目してみました。
今後も気になるスタッツがあれば、実際のプレイヤーと絡めて記事の作成を進めていきたいと思います。
なお、本記事は、記事の最後に紹介している書籍を参考にして作成しています。
それでは、今回のトラッシュトークは以上です。
【参考書籍】
Paola Zuccolotto and Marica Manisera (2020), Basketball Data Science – with Applications in R. Chapman and Hall/CRC. ISBN 9781138600799.
※本書籍の紹介記事を書いていますので、よろしければご参考ください。
山田剛史、杉澤武俊、村井潤一郎(2008)『Rによるやさしい統計学』オーム社.