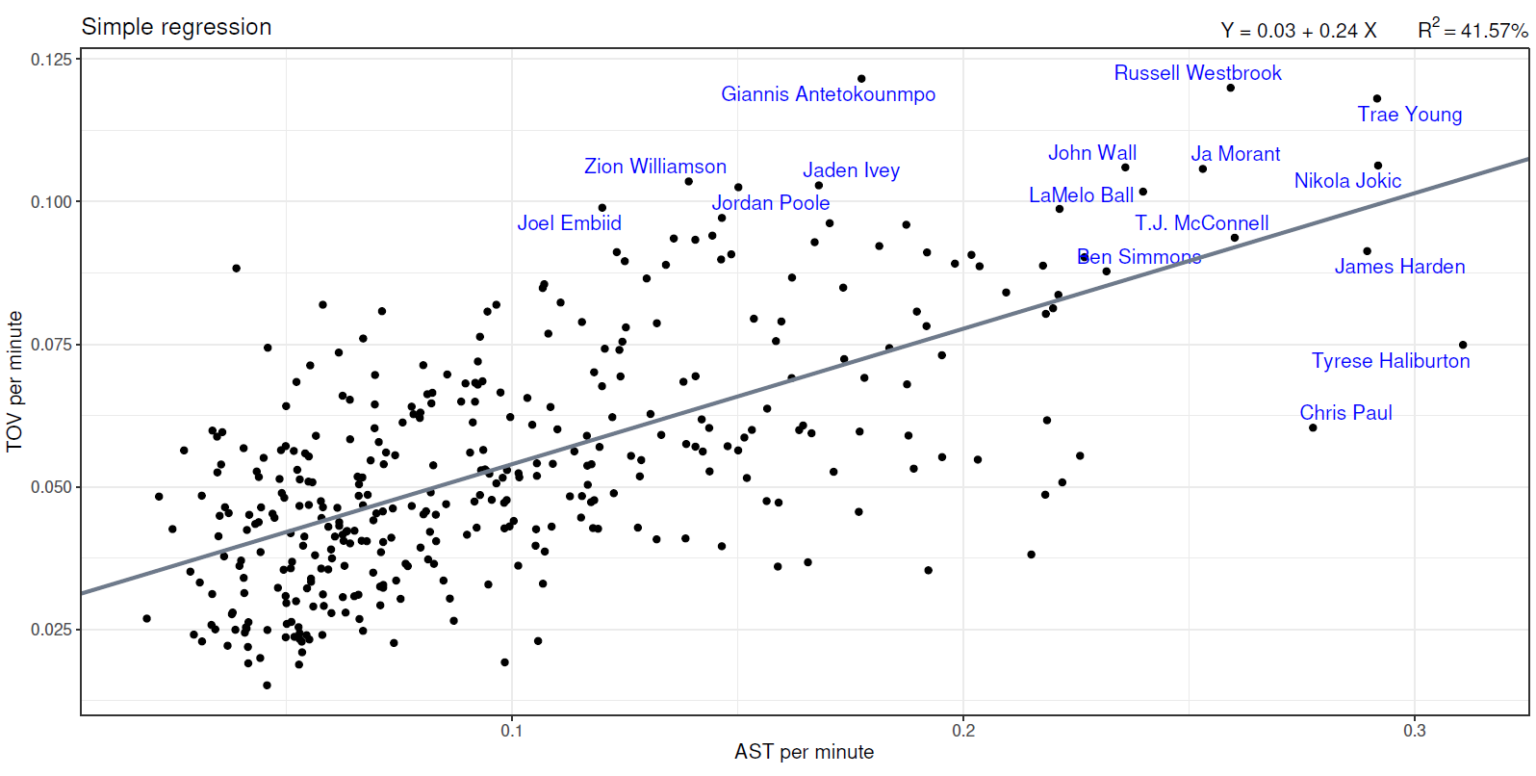
【単回帰分析を用いてNBAにおけるスタッツ間の関係性を確認しよう】2022-23レギュラーシーズンにおけるアシスト数とターンオーバー数を使って両スタッツ間の関係性を把握する

今回は、アシスト数とターンオーバー数を使って、統計ソフトＲによる単回帰分析を実行していきたいと思います。

データは2022–23レギュラーシーズンのPbox（過去記事参照）を使用します。

まずは、今回の単回帰分析で使用する変数と回帰モデルの内容から確認していきます。

※データ分析を実践する際に参考にしている書籍『Basketball Data Science: With Applications in R』の紹介記事も書きましたので、よろしければご確認ください。

単回帰分析で使用する変数と回帰モデル
アシスト数とターンオーバー数を用いた単回帰分析＜NBA2022-23レギュラーシーズン＞
回帰直線の描画＜クリス・ポール、タイリース・ハリバートン、ジェームズ・ハーデンが高パフォーマンス＞
おわりに

単回帰分析で使用する変数と回帰モデル

過去記事で相関行列を扱った際に、2022-23レギュラーシーズンにおける「試合時間1分あたりのアシスト数（AST per MIN）」と「試合時間１分あたりのターンオーバー数（TOV per MIN）」には中程度の正の相関（相関係数0.64）が見られることを述べました。

この点を踏まえ今回の単回帰分析では、独立変数に2022-23レギュラーシーズンの「試合時間1分あたりのアシスト数（AST per MIN）」、従属変数に2022-23レギュラーシーズンの「試合時間１分あたりのターンオーバー数（TOV per MIN）」をそれぞれ使用していきます。（※プレイヤーに関しては、MINが500MIN以上のプレイヤーに限定しています。）

回帰モデルに関しては、「試合時間1分あたりのアシスト数（AST per MIN）」で「試合時間１分あたりのターンオーバー数（TOV per MIN）」を説明することを考え、下記の回帰モデルを想定します。

TOV per MIN＝β₀＋β₁ AST per MIN＋e

β₀は回帰直線の切片、β₁は回帰係数（回帰直線の傾き）、eは残差を表しています。

なお、上記の2変数を算出するコマンドは下記のとおりです。

> library(BasketballAnalyzeR) #パッケージBasketballAnalyzeRの読み込み
> Pbox2223 <- read.csv(file="Pbox_2223.csv") # Pbox2223の読み込み
> Pbox2223.sel <- subset(Pbox2223, MIN>=500) #Pbox2223から出場時間500MIN以上のプレイヤーを抽出
> attach(Pbox2223.sel) #attach()でPbox2223を指定
> X <- AST/MIN #1MINあたりのAST数を算出しXへ格納
> Y <- TOV/MIN #1MINあたりのTOV数を算出しYへ格納
> Pl <- Player #Player欄をPlへ格納
> detach(Pbox2223.sel) #detach()でPbox2223を指定から外す

次に、実際の単回帰分析の結果を確認していきます。

アシスト数とターンオーバー数を用いた単回帰分析＜NBA2022-23レギュラーシーズン＞

「試合時間1分あたりのアシスト数（AST per MIN）」を独立変数、「試合時間１分あたりのターンオーバー数（TOV per MIN）」を従属変数に設定し、統計ソフトRで単回帰分析を実行した結果は下記のとおりです。

> result <- lm(Y~X)
> summary(result)

Call:
lm(formula = Y ~ X)

Residuals:
      Min        1Q    Median        3Q       Max 
-0.043149 -0.011613 -0.001885  0.011943  0.049192 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) 0.030241   0.001689   17.90   <2e-16 ***
X           0.237492   0.014738   16.11   <2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 0.01609 on 365 degrees of freedom
Multiple R-squared:  0.4157,	Adjusted R-squared:  0.4141 
F-statistic: 259.7 on 1 and 365 DF,  p-value: < 2.2e-16

上記の“Coefficients:”以降で示されている“Estimate”の項目を確認すると、回帰直線の切片β₀の推定値は0.030241、回帰係数（回帰直線の傾き）β₁の推定値は0.237492となっていることから、下記の単回帰式が導かれたことがわかります。

TOV per MIN＝0.030241＋0.237492×AST per MIN

上記の単回帰式から、今回使用したデータに関しては、「試合時間1分あたりのアシスト数（AST per MIN）」が1増えた場合、今回のデータでは平均して「試合時間１分あたりのターンオーバー数（TOV per MIN）」が約0.237増加するという傾向を読み取ることができます。

また、“t value”はt値、“Pr(>|t|)”はp値をそれぞれ表しており、今回の場合はβ₀とβ₁の推定値に関して、有意水準0.1%よりも高い水準で有意な結果を得られたことが示されています。

さらに、下部で示されている“Multiple R-squared: 0.4157”は決定係数（今回使用した独立変数を用いて、従属変数の変動をどの程度説明できたのかを示す指標）を表しています。

今回の場合であれば、「試合時間1分あたりのアシスト数（AST per MIN）」を用いて、「試合時間１分あたりのターンオーバー数（TOV per MIN）」の変動を約42%説明できたと解釈することができます。

続いて、今回推定された回帰直線を散布図とともに確認していきます。

回帰直線の描画＜クリス・ポール、タイリース・ハリバートン、ジェームズ・ハーデンが高パフォーマンス＞

今回推定された回帰直線を図示すると、下記のようになります。

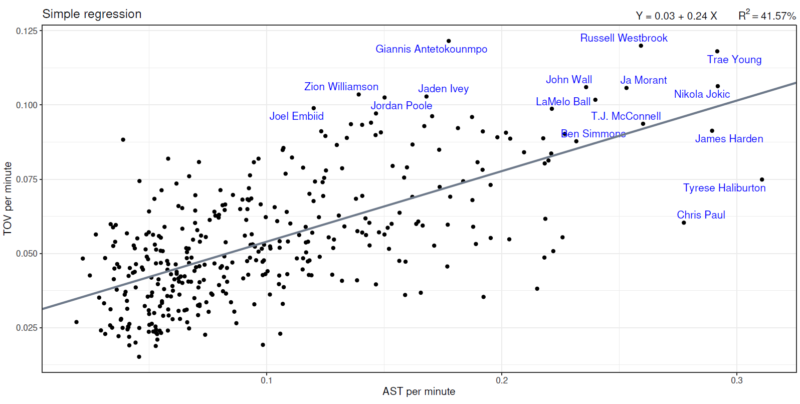
独立変数を”AST per MIN”、従属変数を”TOV per MIN”とした回帰直線＜NBA2022-23レギュラーシーズン＞

横軸は「試合時間1分あたりのアシスト数（AST per MIN）」、縦軸は「試合時間１分あたりのターンオーバー数（TOV per MIN）」が対応しており、実線で示されている直線が今回推定された回帰直線となります。

また、各変数の上位3％に属するプレイヤーに関しては、それぞれそのプレイヤー名が青字で表示されています。

上記のチャートを確認すると、ベン・シモンズとTJ・マッコネルについては、今回推定された回帰直線に極めて近い位置にプロットされていることが分かります。

このことから、この2プレイヤーのアシストとターンオーバーの関係性に関しては、今回の回帰モデルに対してあてはまりが良く、その関係性を上手く説明できたものと解釈することができます。

また、クリス・ポール、タイリース・ハリバートン、ジェームズ・ハーデンについては、回帰直線の下方にプロットされていることから、これらプレイヤーに関しては、そのアシスト数の水準に対して、今回の回帰モデルにより予測されるターンオーバー数よりも少ないターンオーバー数を記録したプレイヤーであることが読み取れます。

その一方で、ジョエル・エンビード、ザイオン・ウイリアムソン、ヤニス・アデトクンボ等については回帰直線の上方にプロットされており、このことは、これらプレイヤーに関しては、そのアシスト数の水準に対して、今回の回帰モデルにより予測されるターンオーバー数よりも多いターンオーバー数を記録したプレイヤーであることを示しています。

なお、上記のチャートを出力するためのコマンドは下記の通りです。

> out <- simplereg(x=X, y=Y, type="lin") #simplereg()を用いて単回帰分析を実行しoutへ格納
> xtitle <- "AST per minute" #x軸のタイトルを設定
> ytitle <- "TOV per minute" #y軸のタイトルを設定
> plot(out, labels=Pl, subset="quant", Lx=0, Ux=0.97, Ly=0, Uy=0.97, xtitle=xtitle, ytitle=ytitle) #各変数上位3%のプレイヤーを表示させ、プロットを出力

おわりに

今回は単回帰分析を用いて、NBA2022-23レギュラーシーズンにおけるアシスト数とターンオーバー数の関係を確認していきました。

回帰分析により得られた回帰係数を用いることで2変数の関係性を数値で捉え、2変数の散布図とともに推定された回帰直線を図示することで、その関係性を視覚的に把握していきました。

過去記事で扱った相違間行列においては、2Pシュート成功数とフリースロー成功数、リバウンド数とブロック数などの組み合わせでも中程度の正の相関を示していることから、これらのスタッツを使用した単回帰分析を行うのも良いかと思います。

なお、本記事は、記事の最後に紹介している書籍を参考にして作成しています。

それでは、今回のトラッシュトークは以上です。

【参考書籍】

Paola Zuccolotto and Marica Manisera (2020), Basketball Data Science – with Applications in R. Chapman and Hall/CRC. ISBN 9781138600799.
※本書籍の紹介記事を書いていますので、よろしければご参考ください。

山田剛史、杉澤武俊、村井潤一郎（2008）『Rによるやさしい統計学』オーム社.

【参考ウェブサイト】

統計WEB．“27-1. 単回帰分析”．統計学の時間．https://bellcurve.jp/statistics/course/27301.html，（参照2023-12-16）.