今回は、PACE、ORtg、Four Factorsを使って、統計ソフトRによるグループ分けをした場合の相関行列の作成方法を紹介していきたいと思います。(※こちらは前回の記事からの続きとなります。まだ前回の記事をご覧になられていない方は、よろしければ下記より前回の記事をご覧ください。)
データは、2022-23レギュラーシーズンのTbox、Obox、Tadd(過去記事参照)を使用します。
まずは、前回の記事でも触れたグループ分けをしていない相関行列とチャートの作成から進めていきたいと思います。
※データ分析を実践する際に参考にしている書籍『Basketball Data Science: With Applications in R』の紹介記事も書きましたので、よろしければご確認ください。
PACE、ORtg、Four Factorsを用いた相関行列<NBA2022-23レギュラーシーズン>
PACE、ORtg、Four Factorsを用いた相関行列とチャートの作成
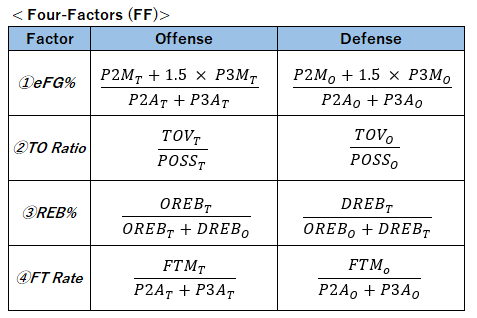
PACE、ORtg、Four Factors(eFG%、TO Ratio、REB%、FT Rate)で作成した相関行列とチャートは下記のとおりです。
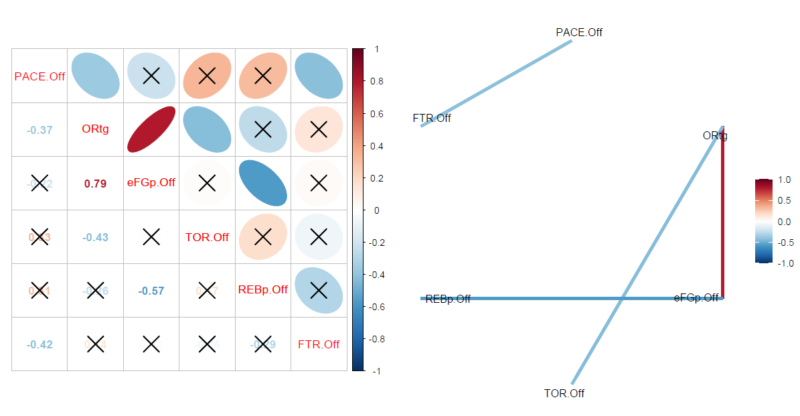
上記の相関行列で示されているスタッツは、いずれもオフェンスに関するスタッツを使用しています。
各スタッツの詳細は過去記事で紹介していますので、よろしければ下記にてご確認ください。
また、上記の相関行列とチャートの見方については前回の記事で紹介していますので、詳細は前回の記事よりご参照ください。
なお、上記で示した相関行列とチャートを出力するためのコマンドは、下記のとおりです。
> library(BasketballAnalyzeR) #パッケージBasketballAnalyzeRの読み込み
> Tbox2223 <- read.csv(file="Tbox_2223.csv") # Tbox2223の読み込み
> Obox2223 <- read.csv(file="Obox_2223.csv") # Obox2223の読み込み
> fourfactors2223 <- fourfactors(Tbox2223, Obox2223) #fourfactors関数でPACE、ORtg、Four Factorsを算出
> attach(fourfactors2223) #attach関数でfourfactors2223を指定
> Y <- data.frame(PACE.Off, ORtg, eFGp.Off=F1.Off, TOR.Off=F2.Off, REBp.Off=F3.Off, FTR.Off=F4.Off)
#必要なスタッツをdata.frame関数でまとめてYに格納
> detach(fourfactors2223) #detach関数でfourfactors2223を指定から外す
> corrmatrixY <- corranalysis(Y[,1:6], threshold=0.4) #Yの1~6列目の変数につき相関行列を作成し、相関係数の絶対値が0.4以上であればチャートで表示する
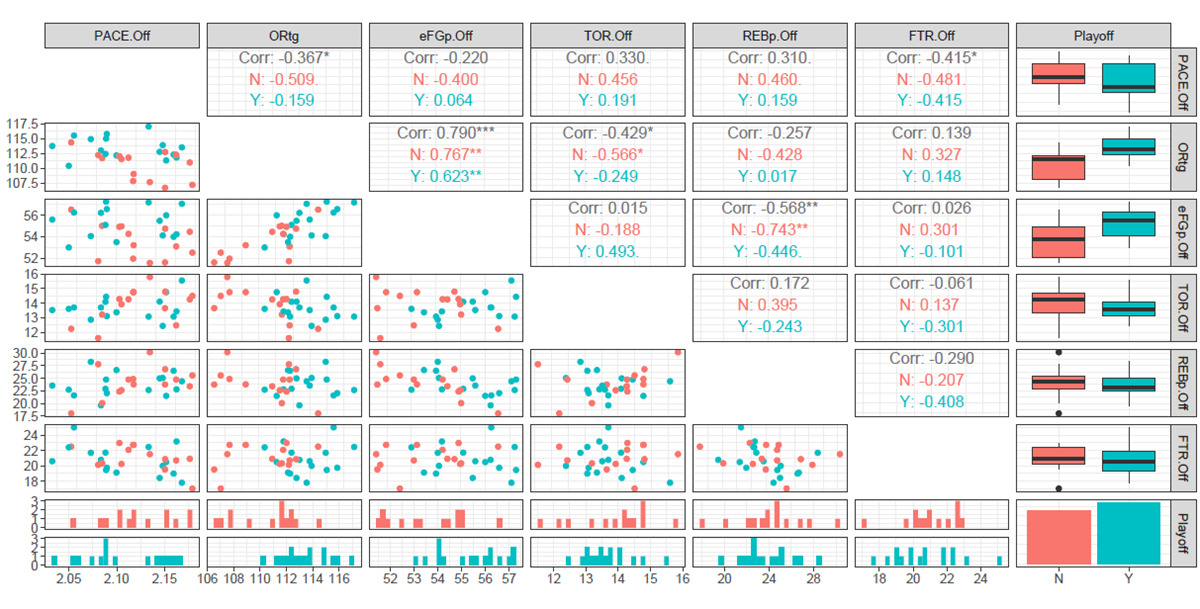
> plot(corrmatrixY) #相関行列とチャートをプロット今回は上記の相関行列につき、プレーオフ進出の有無でチームを2グループに区分した場合の相関行列の作成を進めていきます。
NBA2023プレーオフ進出の有無でグループ分けをした場合の相関行列
プレーオフ進出の有無でグループ分けをした相関行列は、下記のとおりです。
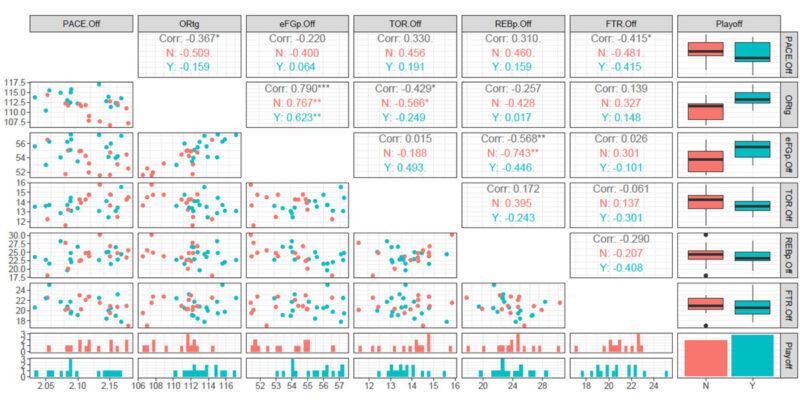
スタッツに関しては、先に示した相関行列と同様のものを使用し、プレーオフ進出なし「N」のグループは赤色で、プレーオフ進出あり「Y」のグループは緑色で表示されています。
上記の相関行列に関しては、対角線上の要素の上三角部分に各スタッツ間の相関係数が示されています。
例えば、ORtgとPACEの相関係数は全体で-0.367、プレーオフ進出なしの場合は-0.509、プレーオフ進出ありの場合は-0.159となります。
なお、相関係数の右上に”*”がついている場合は、相関係数の無相関検定(今回の場合は有意水準5%の両側検定)において、帰無仮説「母集団において相関が0である」が棄却され、対立仮説「母集団において相関は0ではない」が採択されたことを表します。
一方、”*”がついていない場合は、無相関検定において有意な差が認められず、対立仮説「母集団において相関は0ではない」が採択されなかったことを表しています。(無相関検定については前回記事をご参照ください。)
また、上記の相関行列の下三角部分には各スタッツ間の相関図が示され、プレーオフ進出の有無でプロットの色分けがされています。
さらに、下段2行は2グループ別のヒストグラムが表示され、右端の列は2グループ別の箱ひげ図が表示されています。
上記の相関行列に関して、相関の正負と強弱ごとにスタッツの組み合わせをまとめると、下記のようになります。(rは相関係数を表しています。)※1
- 強い正の相関あり(0.7<r≦1.0):eFG%とORtg
- 中程度の負の相関あり(-0.7≦r<-0.4):TO RatioとORtg、REB%とeFG%、FT RateとPACE
- 弱い負の相関あり(-0.4≦r<-0.2):ORtgとPACE
※1 相関関係の強弱の判断に関しては、山田剛史、杉澤武俊、村井潤一郎(2008)『Rによるやさしい統計学』オーム社のp 62 – p64を参考にしています。
相関係数を確認すると、eFG%とORtgの相関係数が0.79と最も高くなっていることから、上記の2スタッツ間の相関の中では、最も強い正の相関を示していることが分かります。
一方、上記の2スタッツ間の相関の中で負の相関が最も強いのは、相関係数-0.568を示すREB%とeFG%であり、次いで、TO RatioとORtgの相関係数-0.429、FT RateとPACEの相関係数-0.415が続きます。
これまで確認した相関関係と相関係数をベースにすると、チームに関しては下記の傾向を読み取ることができます。
- eFG%が高いチームほど、ORtgが高い(オフェンス効率性が高い)傾向があり、TO Ratioが高いチームほど、ORtgが低い(オフェンス効率性が低い)傾向がある。
- REB%.Offが高いチームほど、eFG%が低い傾向がある。(オフェンスリバウンドの強さの裏には、eFG%の低さという欠点が隠れている可能性については、過去記事でも触れています。)
- FT Rateが高いチームほど、PACEが低い傾向がある。
また、相関係数をグループごとに確認すると、すべての相関係数においてプレーオフを進出していない「N」のグループのほうが相関係数の絶対値が大きくなっていることが分かります。(※無相関検定において有意差が認められた相関係数に限ります。)
このことから、上記の各スタッツの組み合わせの相関に関しては、プレーオフに進出していない「N」のグループのほうに直線的な関係がより強く出る傾向があると考えられます。
なお、上記で示した相関行列を出力するためのコマンドは、下記のとおりです。
> Tadd2223 <- read.csv(file="Tadd_2223.csv") # Tadd2223の読み込み
> Playoff <- Tadd2223$Playoff #プレーオフ進出の情報をPlayoffへ格納
> attach(fourfactors2223) #attach関数でfourfactors2223を指定
> YPO <- data.frame(Y, Playoff=Playoff) #Yとプレーオフ進出の情報をdata.frame関数でまとめてYPOに格納
> detach(fourfactors2223) #detach関数でfourfactors2223を指定から外す
> scatterplot(YPO, data.var=1:6, z.var="Playoff", diag=list(continuous="blankDiag")) #相関行列をプロットおわりに
今回は、PACE、ORtg、Four Factorsの相関行列を確認した上で、プレーオフ進出の有無でグループ分けをした場合の相関行列の作成を進めていきました。
グループ分けをすることでグループ別の散布図や相関係数を比較することができ、グループ別のチームの傾向を読み取ることが可能になりました。
今回はプレーオフ進出の有無でグループ分けをしましたが、ポジション別やカンファレンス別などでグループ分けをした場合でも、また違った傾向を読み取ることが出来るかと思います。
なお、本記事は、記事の最後に紹介している書籍を参考にして作成しています。
それでは、今回のトラッシュトークは以上です。
【参考書籍】
Paola Zuccolotto and Marica Manisera (2020), Basketball Data Science – with Applications in R. Chapman and Hall/CRC. ISBN 9781138600799.
※本書籍の紹介記事を書いていますので、よろしければご参考ください。
山田剛史、杉澤武俊、村井潤一郎(2008)『Rによるやさしい統計学』オーム社.