今回は、以下の2つの記事で取り上げた計8つのスタッツを使って、統計ソフトRによる相関行列の作成方法を紹介していきたいと思います。
データは、2022-23レギュラーシーズンのPbox(過去記事参照)を使用し、取り上げるスタッツはP2M、P3M、FTM、REB、AST、STL、BLK、TOVの8つとなります。
それでは相関行列の作成から見ていきたいと思います。
※データ分析を実践する際に参考にしている書籍『Basketball Data Science: With Applications in R』の紹介記事も書きましたので、よろしければご確認ください。
NBA2022-23レギュラーシーズンの基本スタッツの相関
NBAの基本スタッツを用いた相関行列<P3M、AST、TOVなどを使用する>
8つのスタッツで作成した相関行列は下記のとおりです。
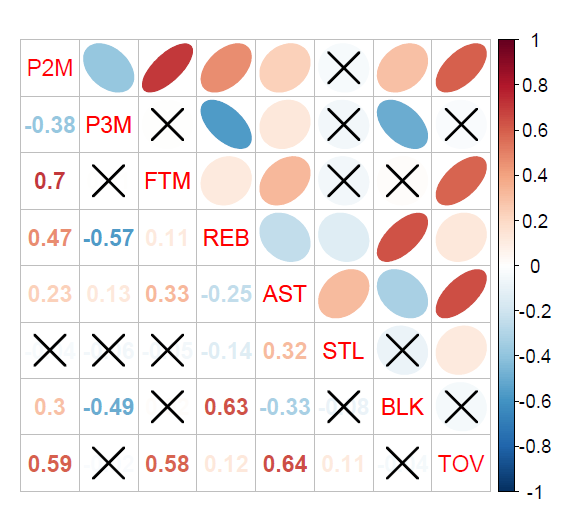
上記の相関行列で示されている各スタッツは、下記のとおりとなっています。(※数値はすべて1MINあたりの数値に変換しています。)
- P2M : 2Pシュート成功数
- P3M : 3Pシュート成功数
- FTM : フリースロー成功数
- REB:オフェンスリバウンドとディフェンスリバウンドの合計数
- AST : アシスト数
- STL : スティール数
- BLK : ブロック数
- TOV : ターンオーバー数
上記の相関行列に関しては、スタッツ名が記載されている対角線上の要素の下三角部分に各スタッツ間の相関係数が示されています。(例えば、P2MとP3Mの相関係数は-0.38、FTMとTOVの相関係数は0.58となります。)
相関行列内の”×”がついている要素については、相関係数の無相関検定において有意な差が認められず、対立仮説「母集団において相関は0ではない」が採択されなかったことを表しています。(無相関検定に関しては後述の箇所を参照ください。)
一方、対角線上の要素の上三角部分は、相関関係の強弱が楕円形と色分けで表されています。
右上がりの楕円形であれば正の相関関係、右下がりの楕円形であれば負の相関関係を表し、楕円形が細くなるほど相関関係が強くなることを示しています。
また、相関係数0は白色で表示され、相関係数が1に近づくにつれ赤色へと変化し、反対に相関係数が-1に近づくと青色へと変化していきます。
上記の相関行列に関して、相関関係の正負と強弱ごとにスタッツをまとめると、下記のようになります。(rは相関係数を表しています。)※1
- 中程度の正の相関あり(0.4<r≦0.7):P2MとFTM、P2MとREB、P2MとTOV、FTMとTOV、REBとBLK、ASTとTOV
- 弱い正の相関あり(0.2<r≦0.4):P2MとAST、P2MとBLK、FTMとAST、ASTとSTL
- 中程度の負の相関あり(-0.7≦r<-0.4):P3MとREB、P3MとBLK
- 弱い負の相関あり(-0.4≦r<-0.2):P2MとP3M、REBとAST、ASTとBLK
- ほとんど相関なし(-0.2≦r≦0.2):P3MとAST、FTMとREB、REBとSTL、REBとTOV、STLとTOV
※1 相関関係の強弱の判断に関しては、山田剛史、杉澤武俊、村井潤一郎(2008)『Rによるやさしい統計学』オーム社のp 62 – p64を参考にしています。
相関係数を確認すると、P2MとFTMの相関係数0.7が最も高くなっており、上記の2スタッツ間の相関関係の中では、最も強い正の相関関係を示していることが分かります。
P2MとFTM の組み合わせの次は、ASTとTOVの相関係数0.64、REBとBLKの相関係数0.63が続きます。
一方、上記の2スタッツ間の相関関係の中で負の相関関係が最も強いのは、相関係数-0.57を示すP3MとREBであり、次いで、P3MとBLKの相関係数-0.49が続きます。
続いて下記に示すチャートは、上記の相関行列内で示されているそれぞれの相関関係を視覚的に捉えやすくしたものとなります
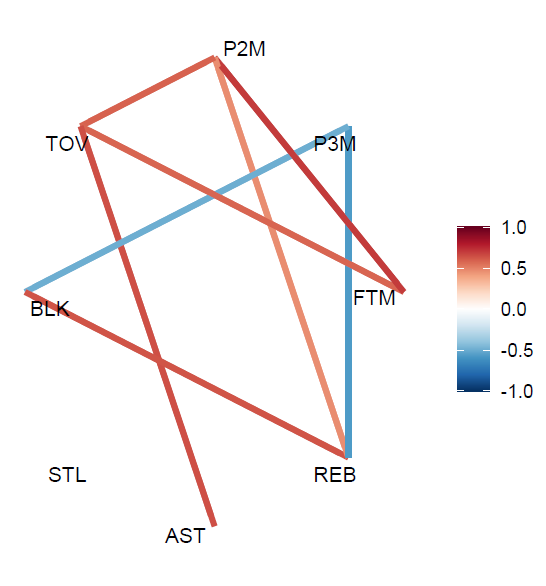
上記のチャートに関しては、中程度以上の相関関係がある組み合わせ(相関係数の絶対値が0.4以上)に限定して、スタッツ間を結ぶラインとその色でそれぞれの相関関係が示されています。
色分けの表示に関しては先に示した相関行列と同様で、相関係数が1に近づくと赤色へ変化し、反対に相関係数が-1に近づくと青色へ変化します。
例えば、FTMに関してはP2MおよびTOVとラインが結ばれていることから、これらの組み合わせは中程度の相関関係を有しており、そのラインの色から正の相関関係であることが把握できます。
また、P3MとREBおよびBLKを結ぶラインに注目すれば、これらの組み合わせは中程度の負の相関関係があることが分かります。
これまで確認した相関関係と相関係数をベースにすると、プレイヤーに関する下記の傾向を読み取ることができます。
- 2Pシュート成功数が多いプレイヤーほど、フリースロー成功数が多い傾向がある。
- アシスト数が多いプレイヤーほど、ターンオーバー数が多い傾向がある。
- リバウンド数が多いプレイヤーほど、ブロック数が多い傾向がある。
- 3Pシュート成功数が多いプレイヤーほど、リバウンド数(またはブロック数)が少ない傾向がある。
なお、上記で示した相関行列とチャートを出力するためのコマンドは、下記のとおりです。
> library(BasketballAnalyzeR) #パッケージBasketballAnalyzeRの読み込み
> Pbox2223 <- read.csv(file="Pbox_2223.csv") # Pbox2223の読み込み
> data2223 <- subset(Pbox2223, MIN>=500) #Pbox2223から出場時間500MIN以上のプレイヤーを抽出
> attach(data2223) #attach関数でPbox2223を指定
> X <- data.frame(P2M, P3M, FTM, REB=(OREB+DREB), AST, STL, BLK, TOV)/MIN #各スタッツのMINあたりの数値をdata.frame関数でまとめてXに格納
> detach(data2223) #detach関数でPbox2223を指定から外す
> corrmatrix <- corranalysis(X[,1:8], threshold=0.4) #Xの1~8列目の変数につき相関行列を作成し、相関係数の絶対値が0.4以上であればチャートで表示する
> plot(corrmatrix) #相関行列とチャートをプロット相関係数の無相関検定について<STLとBLKの実際の相関係数を用いて>
ここでは統計WEBサイト「26-3. 相関係数」や、記事の最後に掲載している書籍を参考の上、無相関検定の内容を簡単に見ていきたいと思います。
無相関検定では、帰無仮説H0を「母集団において相関が0である」、対立仮説H1を「母集団において相関は0ではない」と設定し、以下の算式で算出される検定統計量tに関して、有意水準α%(今回の場合は5%)で両側検定を行うことになります。
$$t=\dfrac{r\sqrt{n-2}}{\sqrt{1-r^{2}}}$$
rは標本相関係数、nはサンプル数を表し、上記の検定統計量tは自由度n-2のt分布に従います。
今回算出したSTLとBLKの相関係数-0.08(表示が薄くて見づらいと思いますが)を使って実際に検定統計量tを計算すると、下記のとおりt=-1.588877となります。
> 標本相関 <- cor(X$STL, X$BLK)
> 標本相関
[1] -0.08287949
> サンプルサイズ <- nrow(X)
> サンプルサイズ
[1] 367
> tの分子 <- 標本相関*sqrt(サンプルサイズ-2)
> tの分子
[1] -1.58341
> tの分母 <- sqrt(1-標本相関^2)
> tの分母
[1] 0.9965596
> t統計量 <- tの分子/tの分母
> t統計量
[1] -1.588877また、自由度365のt分布で下側確率0.025となるtの値をqt関数を利用して求めると、下記のとおり-1.966485となります。
> qt(0.025, 365)
[1] -1.966485以上より、有意水準5%(両側検定)のときの棄却域は、t<-1.966485、t>1.966485となります。
今回、tの実現値は-1.588877であり、この値は棄却域に入らない(-1.588877>-1.966485)ので有意な差は認められず、対立仮説H1は採択されないことになります。(今回の場合、相関行列の対応する要素に”×”がつきます。)
次回について
今回は8つの基本的なスタッツを使って相関行列を作成し、各スタッツ間の相関関係や相関係数をまとめて確認していきました。
相関係数を見ていく際には、無相関検定を行うことで、統計的に有意差が見られた相関係数のみに焦点をあてることができました。
次回記事も引き続き相関関係に焦点をあて、特定のスタッツにつき2つのグループで区分された場合の相関行列の作成方法を見ていきたいと思います。(具体的にはプレーオフ進出の有無でグループ分けした場合の相関行列となります。)
なお、本記事は、記事の最後に紹介している書籍を参考にして作成しています。
それでは、今回のトラッシュトークは以上です。
【参考書籍】
Paola Zuccolotto and Marica Manisera (2020), Basketball Data Science – with Applications in R. Chapman and Hall/CRC. ISBN 9781138600799.
※本書籍の紹介記事を書いていますので、よろしければご参考ください。
山田剛史、杉澤武俊、村井潤一郎(2008)『Rによるやさしい統計学』オーム社.