今回は、獲得点数とアシスト数を使って、統計ソフトRによるジニ係数の算出方法を紹介していきたいと思います。
データは、2022-23レギュラーシーズンのTbox、Pbox、Tadd、PbP. BDB(過去記事参照)を使用します。
はじめに、今回算出していくジニ係数の内容を簡単に確認していきます。
※データ分析を実践する際に参考にしている書籍『Basketball Data Science: With Applications in R』の紹介記事も書きましたので、よろしければご確認ください。
ジニ係数
ここでは、統計WEBサイトの「2-4. ローレンツ曲線」と「2-5. ジニ係数」を参考にしながら、ジニ係数やローレンツ曲線の概要を簡単に見ていきます。
ジニ係数とは、データの分布の偏りや不均等さを測る不平等尺度の一つとなります。
ジニ係数は0から1の間の値をとり、データの偏りが完全に無ければ0、データの偏りが大きくなるにつれて1に近づいていきます。
下図で示すとおり、ジニ係数は完全平等線とローレンツ曲線で囲まれた面積(青色に塗られた部分の面積)の2倍で表されます。(下図ではジニ係数の単位を%で表記しています。)
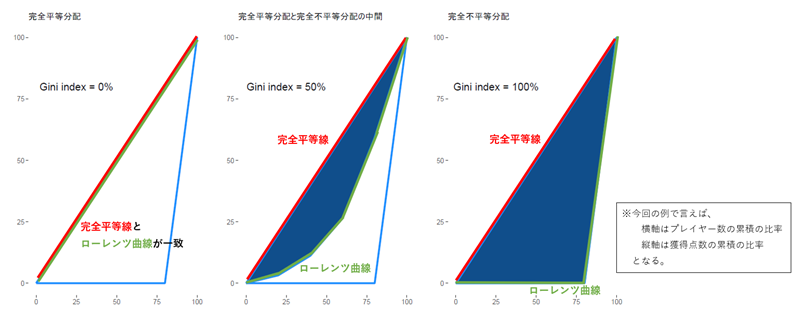
続いて、実際のスタッツを使ってチームの獲得点数に関するジニ係数を算出していきたいと思います。
NBA全30チームの獲得点数に関するジニ係数の散布図<2022-23レギュラーシーズン>
下記がNBA全30チームの獲得点数に関するジニ係数と獲得点数の散布図となります。
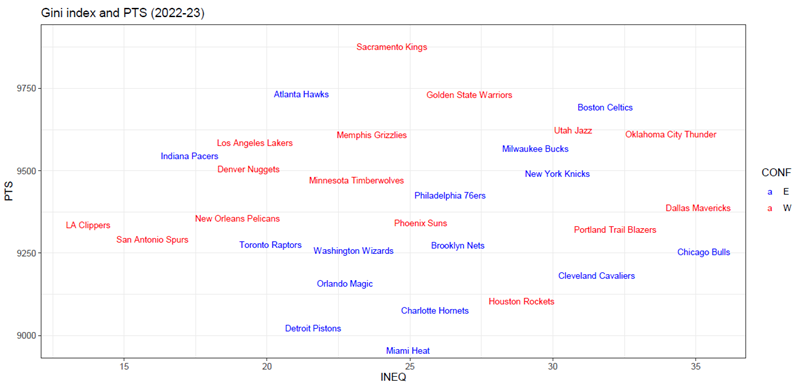
横軸はジニ係数の数値を表し、縦軸はチームの獲得点数を表しています。
また、イースタン・カンファレンスは青色で、ウェスタン・カンファレンスは赤色でそれぞれ表示されています。
なお、各チームのジニ係数と獲得点数の具体的な数値は下記のとおりです。
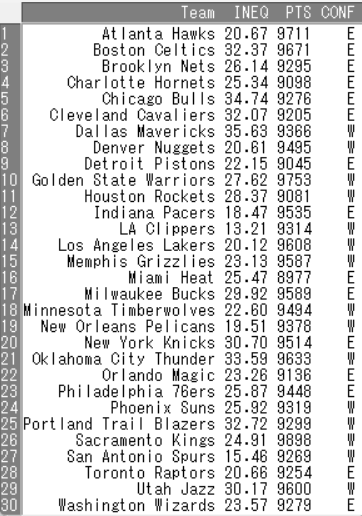
表中のINEQ欄はジニ係数、PTS欄は獲得点数、CONF欄はイースタン・カンファレンス(E)かウェスタン・カンファレンス(W)かを表しています。
上記の散布図を確認すると、以下の理由によりチームのジニ係数と獲得点数の間に関連性は見られないと考えられます。
- サクラメント・キングスとマイアミ・ヒートのジニ係数はそれぞれ24.91%と25.47%で同水準ではあるが、獲得点数はキングスが9,898点、ヒートが8,977点と大きく異なっている。
- ダラス・マーベリックスとロサンゼルス・クリッパーズの獲得点数はそれぞれ9,366点と9,314点で同水準ではあるが、ジニ係数はマーベリックスが35.63%、クリッパーズが13.21%と大きく異なっている。
以上のことから、得点源が少数のプレイヤーに偏っているのか、複数のプレイヤーでバランス良く得点を取るのかは、チームの獲得点数の伸びに影響を与えないものと思われます。
なお、上記の散布図を出力するためのコマンドは下記のとおりです。
> Tbox2223 <- read.csv(file="Tbox_2223.csv") #Tbox2223の読み込み
> Pbox2223 <- read.csv(file="Pbox_2223.csv") #Pbox2223の読み込み
> Tadd2223 <- read.csv(file="Tadd_2223.csv") #Tadd2223の読み込み
> no.teams <- nrow(Tbox2223) #nrow関数でTbox2223の行数をカウントし、no.teamsに格納
> INEQ <- array(0, no.teams) #array関数で0をTbox2223の行数回だけ配列しINEQへ格納
> for (k in 1:no.teams) {
+ Teamk <- Tbox2223$Team[k]
+ Pbox2223.sel <- subset(Pbox2223, Team==Teamk)
+ index <- inequality(Pbox2223.sel$PTS, npl=8)
+ INEQ[k] <- index$Gini
+ }
#変数kの算出を1からno.teamsの行数回だけ繰り返す
#Tbox2223のk行目のTeamをTeamkへ格納(k回繰り返す)
#Pbox2223からTeamkと一致するTeamをPbox2223.selへ格納(k回繰り返す)
#Pbox2223.selのPTS上位8プレイヤーでGini係数を算出しindexへ格納(k回繰り返す)
#indexのGiniの数値をINEQの[k]番目へ格納(k回繰り返す)
> dts <- data.frame(INEQ, PTS=Tbox2223$PTS, CONF=Tadd2223$Conference) #dataframe関数でINEQにPTSとConferenceの情報を追加
> mypal <- colorRampPalette(c("blue","red")) #colorRampPalette関数でパレットを作成
> scatterplot(dts, data.var=c("INEQ","PTS"), z.var="CONF", labels=Tbox2223$Team, palette=mypal, repel_labels=TRUE, title="Gini index and PTS (2022-23)")
#プロットを作成するためのコマンド
次は、チームの中でも特定の5プレイヤーに注目した場合、ジニ係数に何らかの特徴があるのかどうかを確認していきたいと思います。
ラインナップ別の獲得点数に関するジニ係数<ナゲッツの獲得点数の偏りが若干高い>
特定の5プレイヤーに注目した場合の獲得点数に関するジニ係数は、下記となります。
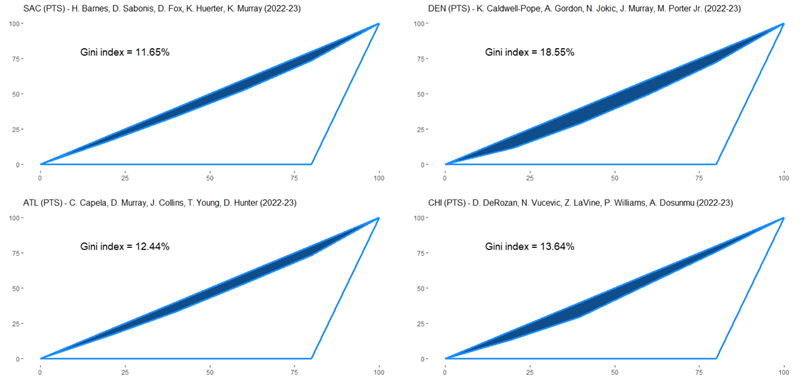
上記の4チームと5プレイヤーのラインナップに関しては、NBA公式ウェブサイトで公表されているラインナップ別のスタッツから、獲得点数上位4番目までのラインナップを選んでいます。
なお、各チームでラインナップされているプレイヤーは下記のとおりです。
- サクラメント・キングス : ハリソン・バーンズ、ドマンタス・サボニス、ディアロン・フォックス、ケビン・ハーター、キーガン・マレー
- デンバー・ナゲッツ : K.コールドウェル・ポープ、アーロン・ゴードン、ニコラ・ヨキッチ、ジャマール・マレー、マイケル・ポーターJr.
- アトランタ・ホークス : クリント・カペラ、デジャンテ・マレー、ジョン・コリンズ、トレイ・ヤング、ディアンドレ・ハンター
- シカゴ・ブルズ : デマー・デローザン、ニコラ・ブーチェビッチ、ザック・ラビーン、パトリック・ウィリアムズ、アヨ・ドスンム
上記の図を確認すると、最もジニ係数が低いのはキングスの11.65%、一方、最もジニ係数が高いのはナゲッツの18.55%であることが分かります。
ホークスとブルズのジニ係数に関しては比較的キングスに近い水準で、それぞれ12.44%と13.64%となっています。
前述したとおり、各チームの獲得点数に関するジニ係数は、15%前後から35%前後の間で数値が算出されていました。
それらのジニ係数と比べると、これらラインナップのジニ係数は全体的に低いため、得点に関しては特定のプレイヤーに過度に偏っているわけではなく、5人が比較的バランス良く得点をしていると考えられます。
なお、上記のジニ係数を出力するためのコマンドは下記のとおりです。
> dts.PbP.2223 <- read.csv(file="PbP. BDB_2223.csv") # PbP. BDB2223の読み込み
> PbP2223 <- PbPmanipulation(dts.PbP.2223) # PbPmanipulation関数でPbP2223を作成
> PbP2223SAC <- subset(PbP2223, team=="SAC") #subset関数でPbP2223からSACの部分を抽出
> lineupSAC <- c("Harrison Barnes", "Domantas Sabonis", "De'Aaron Fox", "Kevin Huerter", "Keegan Murray")
#ラインナップに該当する5名をlineupSACへ格納
> filt5SAC <- apply(PbP2223SAC[, 4:13], 1,
+ function(x) {
+ x <- as.character(x)
+ sum(x %in% lineupSAC)==5
+ })# PbP2223SACの4~13列目の各行につきlineupSACの5名全てが出場している部分を抽出し、filt5SACへ格納
> subPbP2223SAC <- PbP2223SAC[filt5SAC,] #filt5SACに該当する行を抽出しsubPbP2223SACへ格納
> PTS5SAC <- sapply(lineupSAC,
+ function(x) {
+ filtSAC <- subPbP2223SAC$player==x
+ sum(subPbP2223SAC$points[filtSAC], na.rm=T)
+ })# lineupSACに含まれる5プレイヤーごとの合計得点数をsubPbP2223SACのpoints欄から集計(欠損値は無視)し、PTS5SACへ格納
> ineq2223SACPTS5 <- inequality(PTS5SAC, nplayers=5) # inequality関数でPTS5SACを使いジニ係数を算出し、ineq2223SACPTS5へ格納
> pSACPTS5 <- plot(ineq2223SACPTS5, title="SAC (PTS) - Harrison Barnes, Domantas Sabonis, De'Aaron Fox, Kevin Huerter, Keegan Murray (2022-23)")
# plot 関数によりineq2223SACPTS5を使ってジニ係数の図を作成し、pSACPTS5へ格納
#上記のコマンドのSACの部分を全てDEN, ATL, CHIに変え、lineupのc()の中身も各チームの5名に変えれば他チームのジニ係数も算出できる。
> library(gridExtra) #パッケージgridExtraの読み込み
> grid.arrange(pSACPTS5, pDENPTS5, pATLPTS5, pCHIPTS5, nrow=2) # grid.arrange関数で4チームの図を2行でまとめて表示獲得点数に関するジニ係数で見た場合は、偏りがそれほど大きくないことが分かりましたが、アシスト数ではどうでしょうか。
次に、アシストに焦点をあてた場合のジニ係数を算出していきます。
ラインナップ別のアシスト数に関するジニ係数<アシストの偏りが小さいのはブルズ>
特定の5プレイヤーに注目した場合のアシストに関するジニ係数は、下記となります。
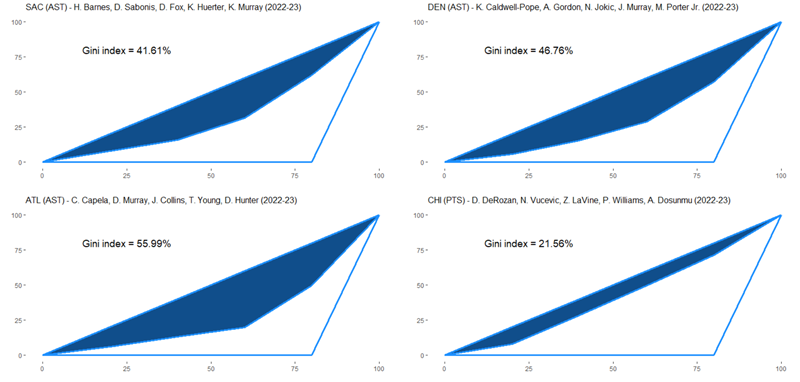
上記の図を確認すると、最もジニ係数が高いのはホークスの55.99%であり、次いで、ナゲッツの46.76%、キングスの41.61%が続きます。
ブルズに関しては他の3チームと比べてジニ係数が低くなっており、その値は21.56%となっています。
前述した獲得点数に関するジニ係数と比較すると、アシストに関するジニ係数は比較的高くなっており、アシストを出すプレイヤーについては、その偏りが大きいことが分かります。
各チームの具体的なアシスト数をプレイヤー別に下記に示しました。

チームごとの状況を確認すると、キングスはドマンタス・サボニスがトップで本数は210本となっており、全体の約37%を占めていることが分かります。
ナゲッツは、ヨキッチがトップで本数は311本であり、全体の約42%を占めています。
ホークスは、トレイ・ヤングがトップで本数は232本であり、全体の約50%を占めています。
一方、比較的ジニ係数の低いブルズのトップはデローザンの94本であり、全体の約28%を占めていることになります。
ジニ係数で判断できる偏りの程度から、キングス、ナゲッツ、ホークスのラインナップに関しては、アシストの出どころが特定のプレイヤーに比較的偏っていることが分かります。
一方、ブルズのほうはアシストの偏りが小さく、その出どころが比較的バランス良く各プレイヤーの間で配分されていることが読み取れます。
なお、上記のジニ係数を出力するためのコマンドは下記のとおりです。
> AST5SAC <- sapply(lineupSAC,
+ function(x) {
+ filt2SAC <- subPbP2223SAC$assist==x
+ table(subPbP2223SAC$assist[filt2SAC])
+ })# lineupSACに含まれる5プレイヤーごとのアシスト数をsubPbP2223SACのassist欄から集計し、AST5SACへ格納
> ineq2223SACAST5 <- inequality(AST5SAC, nplayers=5)
> pSACAST5 <- plot(ineq2223SACAST5, title="SAC (AST) - Harrison Barnes, Domantas Sabonis, De'Aaron Fox, Kevin Huerter, Keegan Murray (2022-23)")
#上記のコマンドのSACの部分を全てDEN, ATL, CHIに変えれば他チームのジニ係数も算出できる。(前述のとおりlineupのc()の中身も各チームの5名に変えていることが前提)
> grid.arrange(pSACAST5, pDENAST5, pATLAST5, pCHIAST5, nrow=2)おわりに
今回は、不平等尺度の1つであるジニ係数を使って、獲得点数とアシストに関する偏りを確認していきました。
チームや特定のラインナップにより算出されるジニ係数は異なり、獲得点数とアシストの偏りの程度は様々であることが分かりました。
今回は、獲得点数とアシスト数に焦点をあてましたが、3ポイントシュートやディフェンスリバウンドなど他のスタッツのジニ係数でも、また違った傾向があると思われます。
なお、本記事は、記事の最後に紹介している書籍を参考にして作成しています。
それでは、今回のトラッシュトークは以上です。
【参考書籍】
Paola Zuccolotto and Marica Manisera (2020), Basketball Data Science – with Applications in R. Chapman and Hall/CRC. ISBN 9781138600799.
※本書籍の紹介記事を書いていますので、よろしければご参考ください。


